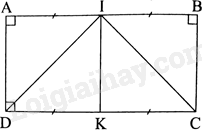
Giải bài 18 trang 74 sách bài tập toán 8 - Chân trời sáng tạoCho hình chữ nhật ABCD có \(AB = 2BC\). Gọi I là trung điểm của AB và K là trung điểm của CD. Chứng minh: Đề bài Cho hình chữ nhật ABCD có \(AB = 2BC\). Gọi I là trung điểm của AB và K là trung điểm của CD. Chứng minh: a) AIKD và BIKC là hình vuông. b) \(IK = \frac{{DC}}{2}\) và \(\widehat {DIC} = {90^0}\). Phương pháp giải - Xem chi tiết a) Sử dụng kiến thức về dấu hiệu nhận biết hình vuông để chứng minh: Hình thoi có một góc vuông là hình vuông. b) Sử dụng kiến thức về tính chất của hình vuông để chứng minh: Trong hình vuông: + Các đường chéo là các đường phân giác của các góc hình vuông + Có 4 góc vuông. Lời giải chi tiết
a) Vì I là trung điểm của AB nên \(AI = IB = \frac{1}{2}AB\) Vì K là trung điểm của CD nên \(DK = CK = \frac{1}{2}DC\) Vì ABCD là hình chữ nhật nên AB//CD, \(AB = CD\), \(AD = BC\) Do đó, \(IA = IB = DK = CK\) Mà \(AB = 2BC\) nên \(IA = IB = DK = CK = AD = BC\) Tứ giác AIKD có: \(DK = AI\), AI//DK nên AIKD là hình bình hành. Mà \(IA = AD\) nên AIKD là hình thoi. Lại có \(\widehat A = {90^0}\) nên AIKD là hình vuông. Tứ giác BIKC có: \(IB = KC\), BI//CK nên BIKC là hình bình hành. Mà \(IB = BC\) nên BIKC là hình thoi. Lại có \(\widehat B = {90^0}\) nên BIKC là hình vuông. b) Vì AIKD là hình vuông nên \(IK = DK = \frac{{DC}}{2}\) và \(\widehat {IDC} = \frac{1}{2}\widehat {ADC} = {45^0}\) Vì BIKC là hình vuông nên \(\widehat {DCI} = \frac{1}{2}\widehat {DCB} = {45^0}\) Tam giác DIC có: \(\widehat {DIC} = {180^0} - \widehat {DCI} - \widehat {CDI} = {90^0}\)
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|