Giải bài 14 trang 74 sách bài tập toán 8 - Chân trời sáng tạoCho hình thang cân ABCD có AB//CD, DB là tia phân giác của góc D, \(DB \bot BC\). Biết \(AB = 4cm\). Tính chu vi của hình thang đó. Đề bài Cho hình thang cân ABCD có AB//CD, DB là tia phân giác của góc D, \(DB \bot BC\). Biết \(AB = 4cm\). Tính chu vi của hình thang đó. Phương pháp giải - Xem chi tiết + Sử dụng kiến thức về chu vi hình thang: Chu vi hình thang bằng tổng độ dài hai đáy và hai cạnh bên của hình đó. + Sử dụng kiến thức về tính chất hình thang cân: Hình thang cân có:
Lời giải chi tiết
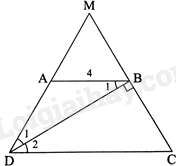
Vì AB//CD nên \(\widehat {{B_1}} = \widehat {{D_2}}\) (hai góc so le trong). Vì DB là tia phân giác của góc ADC nên \(\widehat {{D_1}} = \widehat {{D_2}}\) Do đó, \(\widehat {{B_1}} = \widehat {{D_1}}\) nên tam giác ABD cân tại A, suy ra \(AD = AB = 4cm\) Mà ABCD là hình thang cân nên \(AD = BC = 4cm\) Gọi M là giao điểm của AD và BC. Tam giác MDC có DB vừa là đường phân giác vừa là đường cao nên tam giác MDC cân tại D nên \(\widehat M = \widehat C\) Mà \(\widehat C = \widehat {ADC}\) (do ABCD là hình thang cân) nên \(\widehat C = \widehat {ADC} = \widehat M\). Suy ra, tam giác MDC là tam giác đều. Suy ra: \(DC = MC = 2BC = 8cm\) Chu vi hình thang ABCD là: \(AB + BC + CD + DA = 20cm\)  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
