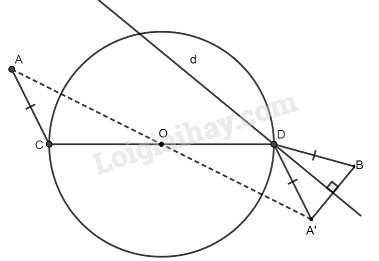
Bài 14* trang 158 SBT toán 9 tập 1Giải bài 14* trang 158 sách bài tập toán 9. Cho đường tròn (O) và hai điểm A, B nằm bên ngoài đường tròn. Dựng đường kính COD sao cho AC = BD... Đề bài Cho đường tròn (O) và hai điểm \(A, B\) nằm bên ngoài đường tròn. Dựng đường kính \(COD\) sao cho \(AC = BD.\) Phương pháp giải - Xem chi tiết Sử dụng tính chất đường trung trực của đoạn thẳng. Các bước dựng hình: + Dựng điểm \(A'\) đối xứng với \(A\) qua \(O.\) + Dựng đường trung trực d của \(A'B\), cắt (O) tại \(D\). + Dựng đường kính \(COD\). Lời giải chi tiết
* Cách dựng − Dựng \(A'\) đối xứng với \(A\) qua tâm \(O\) của đường tròn. − Dựng đường thẳng \(d\) là đường trung trực của \(A’B.\) − Gọi giao điểm của đường thẳng \(d\) và đường tròn (O) là \(D.\) − Dựng đường kính \(COD.\) * Chứng minh Ta có: \(OA = OA’\) (do A và A' đối xứng nhau qua O) và \(OD = OC\) (do C, D cùng thuộc đường tròn (O)) Suy ra tứ giác \(ACA’D\) là hình bình hành (vì có hai đường chéo AA' và CD giao nhau tại trung điểm O của mỗi đường) Suy ra: \(AC = A’D\) (tính chất hình bình hành) Lại có: \(A’D = DB\) (tính chất đường trung trực) Suy ra: \(AC = BD.\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|
