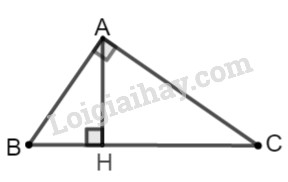
Bài 13* trang 158 SBT toán 9 tập 1Giải bài 13* trang 158 sách bài tập toán 9. Tam giác ABC cân tại A, BC = 12cm, đường cao AH = 4cm. Tính bán kính của đường tròn ngoại tiếp tam giác ABC. Đề bài Tam giác \(ABC\) cân tại \(A\), \(BC = 12cm\), đường cao \(AH = 4cm\). Tính bán kính của đường tròn ngoại tiếp tam giác \(ABC.\) Phương pháp giải - Xem chi tiết + Đường tròn ngoại tiếp của tam giác là đường tròn đi qua tất cả các đỉnh của tam giác. + Xét tam giác ABC vuông tại A, có đường cao AH:
- Áp dụng định lí Pytago: \(B{C^2} = A{B^2} + A{C^2}\) - Hệ thức lượng trong tam giác vuông: \(A{H^2} = BH.HC\) Lời giải chi tiết
Kéo dài đường cao \(AH\) cắt đường tròn ngoại tiếp tam giác \(ABC\) tại \(D\). Gọi \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC.\) Vì tam giác \(ABC\) cân tại \(A\) nên \(AH\) vừa là đường cao vừa là đường trung trực của \(BC\). Suy ra \(AD\) là đường trung trực của \(BC\) và H là trung điểm của BC. Khi đó \(O\) thuộc \(AD\) hay \(AD\) là đường kính của đường tròn ngoại tiếp tam giác \(ABC\). Tam giác \(ACD\) nội tiếp trong (O) có \(AD\) là đường kính suy ra: \(\widehat {ACD} = 90^\circ \) Tam giác \(ACD\) vuông tại \(C\) nên theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: \(C{H^2} = HA.HD\) Suy ra: \(HD = \dfrac{{C{H^2}}}{{HA}} = \dfrac{{{{\left( {\dfrac{{BC}}{2}} \right)}^2}}}{{HA}}\)\( = \dfrac{{{{\left( {\dfrac{{12}}{2}} \right)}^2}}}{4} = \dfrac{{{6^2}}}{4} = \dfrac{{36}}{4} = 9\) Ta có: \(AD = AH +HD = 4 + 9 = 13\) (cm) Vậy bán kính của đường tròn (O) là: \(R = \dfrac{{AD}}{ 2} = \dfrac{{13}}{2} = 6,5\) (cm) HocTot.Nam.Name.Vncom  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
