Bài 126 trang 96 SBT toán 8 tập 1Giải bài 126 trang 96 sách bài tập toán 8. Cho tam giác ABC, điểm M di chuyển trên cạnh BC. Gọi I là trung điểm của AM. Điểm I di chuyển trên đường nào ? Đề bài Cho tam giác ABC, điểm M di chuyển trên cạnh BC. Gọi I là trung điểm của AM. Điểm I di chuyển trên đường nào ? Phương pháp giải - Xem chi tiết Ta sử dụng kiến thức: +) Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba. +) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy. +) Các điểm cách đường thẳng b một khoảng bằng h nằm trên hai đường thẳng song song với b và cách b một khoảng bằng h. Lời giải chi tiết
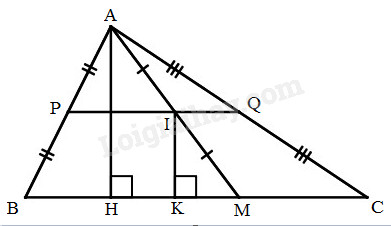
Kẻ AH⊥BC, IK⊥BC ⇒AH//IK Trong tam giác AHM ta có: AI=IM(gt) IK//AH (chứng minh trên) Nên K là trung điểm của HM (đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba) Suy ra: IK là đường trung bình của ∆AHM ⇒IK=12AH ∆ABC cố định nên AH không thay đổi ⇒IK=12AH không đổi. I thay đổi cách BC một khoảng bằng AH2 không đổi nên I nằm trên đường thẳng song song với BC, cách BC một khoảng bằngAH2. Khi M trùng với điểm B thì I trùng với P là trung điểm của AB. Khi M trùng với điểm C thì I trùng với Q là trung điểm của AC. Vậy khi M chuyển động trên cạnh BC của ∆ABC thì trung điểm I của AM chuyển động trên đường trung bình PQ của ∆ABC. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|
