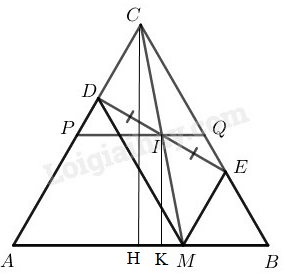
Bài 129 trang 96 SBT toán 8 tập 1

Đề bài

Cho đoạn thẳng $AB,$ điểm $M$ di chuyển trên đoạn thẳng ấy. Vẽ về một phía của $AB$ các tam giác đều $AMD, BME.$ Trung điểm $I$ của $DE$ di chuyển trên đường nào $?$

Lời giải chi tiết

Gọi giao điểm của $AD$ và $BE$ là $C.$

$∆ ABC$ có: $\widehat A = {60^0}$ (vì $∆ ADM$ đều)

                  $\widehat B = {60^0}$ (vì $∆ BEM$ đều)

Suy ra: $∆ ABC$ đều

Do đó $AC = AB = BC$ nên điểm $C$ cố định

$\widehat A = \widehat {EMB} = {60^0}$

$⇒ ME // AC$ (vì có cặp góc đồng vị bằng nhau)

hay $ME // DC$

$\widehat {DMA} = \widehat B = {60^0}$ (vì tam giác ADM đều và tam giác ABC đều)

$⇒ MD // BC$ (vì có cặp góc đồng vị bằng nhau)

hay $MD // EC$

Tứ giác $CDME$ là hình bình hành

$I$ là trung điểm của $DE$ nên $I$ là trung điểm của $CM$

Kẻ $CH ⊥ AB, IK ⊥ AB$ $⇒ IK // CH$

Trong $∆ CHM$ ta có:

$CI = IM$

$IK // CH$

Nên K là trung điểm của HM.

Suy ra $IK$ là đường trung bình của $∆ CHM$ $⇒ IK = \displaystyle {1 \over 2}CH$

$C$ cố định $⇒ CH$ không đổi $⇒ IK =\displaystyle{1 \over 2}CH$ không thay đổi nên $I$ chuyển động trên đường thẳng song song $AB,$ cách $AB$ một khoảng bằng $\displaystyle{1 \over 2}CH.$

Khi $M$ trùng với $A$ thì $I$ trùng trung điểm $P$ của $AC.$

Khi $M$ trùng với $B$ thì $I$ trùng với trung điểm $Q$ của $BC.$

Vậy khi $M$ chuyển động trên đoạn thẳng $AB$ thì $I$ chuyển động trên đoạn $PQ$ ($P$ là trung điểm của $AC, Q$ là trung điểm của $BC$)

HocTot.Nam.Name.Vn