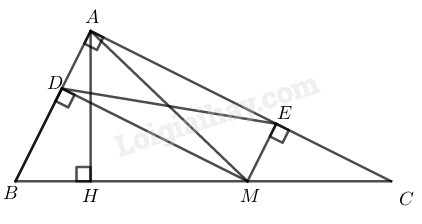
Bài 127 trang 96 SBT toán 8 tập 1Bài 127 trang 96 sách bài tập toán 8. Cho tam giác ABC vuông tại A, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC... Đề bài Cho tam giác ABC vuông tại A, điểm M thuộc cạnh BC. Gọi D,E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB,AC. a) So sánh các độ dài AM,DE. b) Tìm vị trí của điểm M trên cạnh BC để DE có độ dài nhỏ nhất. Phương pháp giải - Xem chi tiết Sử dụng kiến thức: +) Tứ giác có ba góc vuông là hình chữ nhật. +) Trong hình chữ nhật, hai đường chéo bằng nhau. +) Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất. Lời giải chi tiết
a) Xét tứ giác ADME ta có: ˆA=900 (gt) MD⊥AB(gt) ⇒^MDA=900 ME⊥AC(gt) ⇒^MEA=900 Suy ra: Tứ giác ADME là hình chữ nhật (vì có ba góc vuông) ⇒AM=DE (tính chất hình chữ nhật) b) Ta có: AH⊥BC nên AM≥AH (quan hệ đường vuông góc và đường xiên) Dấu “=” xảy ra khi M trùng với H. Mà DE=AM (chứng minh trên) Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường vuông góc kẻ từ A đến BC. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|
