Đề thi học kì 2 Toán 11 - Đề số 2Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.Đề bài
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Cho hàm số \(f(x) = \frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6.\) Phương trình \(f'(x) = 0\) có nghiệm là
Câu 2 :
Gọi (d) là tiếp tuyến của đồ thị hàm số\(y = f(x) = - {x^3} + x\) tại điểm \(M( - 2;6).\) Phương trình của (d) là
Câu 3 :
Tính \(\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1} - 2}}{{9 - {x^2}}}\) bằng
Câu 4 :
Cho \(u = u\left( x \right),v = v\left( x \right),v\left( x \right) \ne 0\); với k là hằng số. Hãy chọn khẳng định sai?
Câu 5 :
Đạo hàm của hàm số \(y = \frac{{2x - 1}}{{1 - x}}\) là
Câu 6 :
Cho hàm số: \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\quad khi\;x \ne 1\\m\quad \quad \quad khi\;x = 1\end{array} \right.\) . Để f(x) liên tục tại điểm \({x_0} = 1\)thì m bằng:
Câu 7 :
Tìm đạo hàm của hàm số sau \(y = {x^4} - 3{x^2} + 2x - 1\)
Câu 8 :
Cho hàm số \(f(x) = \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}},(a \in R,a \ne 0)\). Khi đó \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) bằng
Câu 9 :
Cho hình chóp \(S.ABC\) có đáy ABC là tam giác vuông tại B và SA vuông góc mặt đáy \(\left( {ABC} \right)\), \(SB = 2a\), \(AB = a\)( tham khảo hình vẽ). Tính góc giữa SB và \(mp\left( {ABC} \right)\)
Câu 10 :
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng?
Câu 11 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Khẳng định nào sau đây đúng ?
Câu 12 :
Với hàm số \(g\left( x \right) = \frac{{\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{x - 1}};\,g'\left( 2 \right)\) bằng
Phần II. Câu trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi a) Xác suất để 3 viên bi lấy ra đều màu đỏ là \(\frac{{14}}{{285}}\)
Đúng
Sai
b) Xác suất để 3 viên bi lấy ra có không quá hai màu là \(\frac{{43}}{{57}}\)
Đúng
Sai
c) Xác suất để 3 viên bi lấy ra đều có màu vàng là \(\frac{1}{7}\)
Đúng
Sai
d) Xác suất để 3 viên bi lấy ra có đủ cả ba màu là \(\frac{{14}}{{57}}\)
Đúng
Sai
Câu 2 :
Cho hàm số có đồ thị (C): \(y = f(x) = \frac{{x - 2}}{{x - 1}}\) a) Phương trình tiếp tuyến của (C) tại điểm M có tung độ bằng 4 là : \(y = 9x - 2\)
Đúng
Sai
b) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục hoành là\(y = x + 2\)
Đúng
Sai
c) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục tung là:\(y = x + 2\)
Đúng
Sai
d) Phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng \((d):y = - x + 1\) là \(y = - \frac{2}{5}x + 1\)
Đúng
Sai
Câu 3 :
Cho hình chóp S.ABC có SA ⊥ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC. a) \(d((MNP),(ABC)) = h\)
Đúng
Sai
b) \(d(NP,(ABC)) = \frac{h}{2}\)
Đúng
Sai
c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
Đúng
Sai
d) \((MNP)//(ABC)\)
Đúng
Sai
Câu 4 :
Cho hàm số \(y = \sin x\) a) Đạo hàm của hàm số là \(y' = - cosx\)
Đúng
Sai
b) Biểu thức \(y'(\frac{\pi }{2}) = 0\)
Đúng
Sai
c) Biểu thức \(y''(\frac{\pi }{2}) = 0\)
Đúng
Sai
d) Biểu thức \({y^{(2024)}} = \sin (x + 1012\pi )\)
Đúng
Sai
Phần III. Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6
Lời giải và đáp án
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Cho hàm số \(f(x) = \frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6.\) Phương trình \(f'(x) = 0\) có nghiệm là
Đáp án : C Phương pháp giải :
Sử dụng công thức đạo hàm. Lời giải chi tiết :
\(\begin{array}{l}f'(x) = (\frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6)' = {x^2} - 3x - 4\\f'(x) = 0\,\,hay\,\,{x^2} - 3x - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 4\end{array} \right.\end{array}\) Đáp án C.
Câu 2 :
Gọi (d) là tiếp tuyến của đồ thị hàm số\(y = f(x) = - {x^3} + x\) tại điểm \(M( - 2;6).\) Phương trình của (d) là
Đáp án : C Phương pháp giải :
Phương trình tiếp tuyến với đồ thị (C): \(y = f(x)\)tại điểm \(M({x_0};f({x_0}))\)là: \(y = f'({x_0})(x - {x_0}) + f({x_0})\) Trong đó: \(M({x_0};f({x_0}))\)gọi là tiếp điểm. \(k = f'({x_0})\)là hệ số góc. Lời giải chi tiết :
\(y' = f'(x) = ( - {x^3} + x)' = - 3{x^2} + 1\) Phương trình tiếp tuyến của đồ thị \(y = f(x) = - {x^3} + x\) tại điểm \(M( - 2;6).\) \(y = f'( - 2)(x + 2) + 6\,\,hay\,\,y = - 11(x + 2) + 6 = - 11x - 16\) Đáp án C.
Câu 3 :
Tính \(\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1} - 2}}{{9 - {x^2}}}\) bằng
Đáp án : A Phương pháp giải :
Nhận biết dạng vô định \(\frac{0}{0}\): Tính \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x)}}{{g(x)}}\)trong đó \(f(x{}_0) = g({x_0}) = 0\) Khử dạng vô định \(\frac{0}{0}\): Phân tích tử thức và mẫu thức sao cho xuất hiện nhân tử chung \((x - {x_0})\) Lời giải chi tiết :
\(\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1} - 2}}{{9 - {x^2}}} = \mathop {\lim }\limits_{x \to 3} \frac{{x - 3}}{{(\sqrt {x + 1} + 2)(9 - {x^2})}} = \mathop {\lim }\limits_{x \to 3} \frac{{ - 1}}{{(\sqrt {x + 1} + 2)(3 + x)}} = \frac{{ - 1}}{{24}}\) Đáp án A.
Câu 4 :
Cho \(u = u\left( x \right),v = v\left( x \right),v\left( x \right) \ne 0\); với k là hằng số. Hãy chọn khẳng định sai?
Đáp án : A Phương pháp giải :
Áp dụng công thức tính đạo hàm Lời giải chi tiết :
\({\left( {\frac{1}{v}} \right)^\prime } = - \frac{{v'}}{{{v^2}}}\) \(\left( {u + v} \right)' = u' + v'\) \({\left( {k.u} \right)^\prime } = k.u'\) \(\left( {u.v} \right)' = u'.v + u.v'\) Đáp án A.
Câu 5 :
Đạo hàm của hàm số \(y = \frac{{2x - 1}}{{1 - x}}\) là
Đáp án : B Phương pháp giải :
Sử dụng công thức tính đạo hàm của hàm phân thức: \(y' = \left( {\frac{{ax + b}}{{cx + d}}} \right)' = \frac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\) Lời giải chi tiết :
\(y' = \left( {\frac{{2x - 1}}{{1 - x}}} \right)' = \left( {\frac{{2x - 1}}{{ - x + 1}}} \right)' = \frac{{2.1 - ( - 1).( - 1)}}{{{{( - x + 1)}^2}}} = \frac{1}{{{{( - x + 1)}^2}}}\) Đáp án B.
Câu 6 :
Cho hàm số: \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\quad khi\;x \ne 1\\m\quad \quad \quad khi\;x = 1\end{array} \right.\) . Để f(x) liên tục tại điểm \({x_0} = 1\)thì m bằng:
Đáp án : C Phương pháp giải :
Bước 1: Tính f(x0) = f2(x0). Bước 2: Tính \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = \mathop {\lim }\limits_{x \to {x_0}} {f_1}(x) = L\) Bước 3: Nếu f2(x0) = L thì hàm số f(x) liên tục tại x0. Nếu f2(x0) ≠ L thì hàm số f(x) không liên tục tại x0. (Đối với bài toán tìm tham số m để hàm số liên tục tại x0, ta thay bước 3 thành: Giải phương trình L = f2(x0), tìm m) Lời giải chi tiết :
Hàm số đã cho xác định trên R Ta có: \(\begin{array}{l}f(1) = m\\\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)(x + 1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} (x + 1) = 2\end{array}\) Ta thấy \(\mathop {\lim }\limits_{x \to 1} f(x) = f(1)\) Nên m = 2 Vậy khi m = 2 thì hàm số liên tục tại \({x_0} = 1\) Đáp án C.
Câu 7 :
Tìm đạo hàm của hàm số sau \(y = {x^4} - 3{x^2} + 2x - 1\)
Đáp án : D Phương pháp giải :
Sử dụng công thức tính đạo hàm của hàm hợp Lời giải chi tiết :
\(y' = \left( {{x^4} - 3{x^2} + 2x - 1} \right)' = 4{x^3} - 6x + 2\) Đáp án D.
Câu 8 :
Cho hàm số \(f(x) = \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}},(a \in R,a \ne 0)\). Khi đó \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) bằng
Đáp án : A Phương pháp giải :
Nhận dạng: \(\mathop {\lim }\limits_{x \to \pm \infty } \frac{{f(x)}}{{g(x)}} = \)\(\frac{\infty }{\infty }\) với \(\mathop {\lim }\limits_{x \to \pm \infty } f(x) = \pm \infty ,\mathop {\lim }\limits_{x \to \pm \infty } g(x) = \pm \infty \) TH1: Nếu f(x) , g(x) là các đa thức thì chia cả tử và mẫu cho lũy thừa cao nhất của x. TH2: Nếu f(x) , g(x) chứa căn thì có thể chia cả tử và mẫu cho lũy thừa cao nhất của x hoặc nhân lượng liên hợp Lời giải chi tiết :
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2}(a + \frac{4}{x} + \frac{3}{{{x^2}}})}}{{{x^2}(\frac{3}{x} - 2a)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{a + \frac{4}{x} + \frac{3}{{{x^2}}}}}{{\frac{3}{x} - 2a}} = \frac{a}{{ - 2a}} = - \frac{1}{2}\) Đáp án A.
Câu 9 :
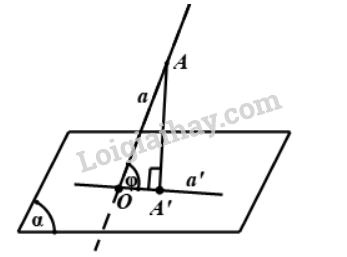
Cho hình chóp \(S.ABC\) có đáy ABC là tam giác vuông tại B và SA vuông góc mặt đáy \(\left( {ABC} \right)\), \(SB = 2a\), \(AB = a\)( tham khảo hình vẽ). Tính góc giữa SB và \(mp\left( {ABC} \right)\)
Đáp án : B Phương pháp giải :
Bước 1: Tìm giao điểm O của đường thẳng a và \(\left( \alpha \right)\) Bước 2: Xác định hình chiếu A’ của một điểm \(A \in \left( \alpha \right)\) xuống \(\left( \alpha \right)\) Bước 3: Suy ra: \((a;\left( \alpha \right)) = (a;a') = \widehat {AOA'}\) Lời giải chi tiết :
Do \(SA \bot (ABC)\) nên A là hình chiếu của S lên (ABC) Ta có: \((SB,(ABC)) = (SB,AB) = \widehat {SBA}\) Xét \(\Delta SAB:c{\rm{os}}\widehat {SBA} = \frac{{AB}}{{SB}} = \frac{a}{{2a}} = \frac{1}{2}\) Suy ra: \(\widehat {SBA} = {60^0}\) Đáp án B.
Câu 10 :
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng?
Đáp án : B Phương pháp giải :
Sử dụng định lý đường thẳng vuông góc với mặt phẳng và hai mặt phẳng vuông góc với nhau Lời giải chi tiết :
Ta có: \(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\,(do\,\,SA \bot (ABC{\rm{D}}))\\AD,SA \subset (SAD)\\AD \cap SA\end{array} \right. \Rightarrow CD \bot (SAD)\) Mặt khác: \(CD \subset (SCD) \Rightarrow (SCD) \bot (SAD)\) Đáp án B.
Câu 11 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Khẳng định nào sau đây đúng ?
Đáp án : C Phương pháp giải :
Sử dụng định lý đường thẳng vuông góc với mặt phẳng Lời giải chi tiết :
Ta có: \(\left\{ \begin{array}{l}AC \bot BD\\AC \bot SO\\BD,SO \subset (SBD)\\BD \cap SO\end{array} \right. \Rightarrow AC \bot (SBD)\) Đáp án C.
Câu 12 :
Với hàm số \(g\left( x \right) = \frac{{\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{x - 1}};\,g'\left( 2 \right)\) bằng
Đáp án : B Phương pháp giải :
Sử dụng phương tính đạo hàm của hàm hợp Lời giải chi tiết :
\(\begin{array}{l}g'\left( x \right) = \frac{{\left[ {\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}} \right]'(x - 1) - \left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}.(x - 1)'}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{\left[ {2{{\left( {2 - 3x} \right)}^2} + (2x + 1).2\left( {2 - 3x} \right).( - 3)} \right] + \left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{{{\left( {x - 1} \right)}^2}}}\\ = \frac{{3x(3x - 2)(4x - 5)}}{{{{\left( {x - 1} \right)}^2}}}\\ \Rightarrow g'\left( 2 \right) = \frac{{3x(3x - 2)(4x - 5)}}{{{{\left( {x - 1} \right)}^2}}} = 72\end{array}\) Đáp án B.
Phần II. Câu trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi a) Xác suất để 3 viên bi lấy ra đều màu đỏ là \(\frac{{14}}{{285}}\)
Đúng
Sai
b) Xác suất để 3 viên bi lấy ra có không quá hai màu là \(\frac{{43}}{{57}}\)
Đúng
Sai
c) Xác suất để 3 viên bi lấy ra đều có màu vàng là \(\frac{1}{7}\)
Đúng
Sai
d) Xác suất để 3 viên bi lấy ra có đủ cả ba màu là \(\frac{{14}}{{57}}\)
Đúng
Sai
Đáp án
a) Xác suất để 3 viên bi lấy ra đều màu đỏ là \(\frac{{14}}{{285}}\)
Đúng
Sai
b) Xác suất để 3 viên bi lấy ra có không quá hai màu là \(\frac{{43}}{{57}}\)
Đúng
Sai
c) Xác suất để 3 viên bi lấy ra đều có màu vàng là \(\frac{1}{7}\)
Đúng
Sai
d) Xác suất để 3 viên bi lấy ra có đủ cả ba màu là \(\frac{{14}}{{57}}\)
Đúng
Sai
Phương pháp giải :
Sử dụng các quy tắc đếm để xác định số phần tử của không gian mẫu và biến cố Lời giải chi tiết :
Không gian mẫu: \((\Omega ) = C_{20}^3 = 1140\) a) Gọi A là biến cố: “3 viên bi lấy ra đều màu đỏ”; \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{C_8^3}}{{C_{20}^3}} = \frac{{56}}{{1140}} = \frac{{14}}{{285}}\) b) B là biến cố: “3 viên bi lấy ra có không quá hai màu” TH1: Số cách lấy ra 3 viên bi lấy ra chỉ có một màu: \(C_8^3 + C_7^3 + C_5^3 = 101\) TH2: Số cách lấy ra 3 viên bi lấy ra chỉ có đúng hai màu: \(\left[ {C_{15}^3 - \left( {C_8^3 + C_7^3} \right)} \right] + \left[ {C_{13}^3 - \left( {C_8^3 + C_5^3} \right)} \right] + \left[ {C_{12}^3 - \left( {C_5^3 + C_7^3} \right)} \right] = 759\) Nên: \(P(B) = \frac{{n(B)}}{{n(\Omega )}} = \frac{{101 + 759}}{{1140}} = \frac{{43}}{{57}}\) c) C là biến cố: “3 viên bi lấy ra đều có màu vàng”; \(P(C) = \frac{{n(C)}}{{n(\Omega )}} = \frac{{C_5^3}}{{C_{20}^3}} = \frac{{10}}{{1140}} = \frac{1}{{114}}\) d) D là biến cố: “3 viên bi lấy ra có đủ cả ba màu”: \(P(D) = \frac{{n(D)}}{{n(\Omega )}} = \frac{{C_8^1.C_7^1.C_5^1}}{{C_{20}^3}} = \frac{{280}}{{1140}} = \frac{{14}}{{57}}\)
Câu 2 :
Cho hàm số có đồ thị (C): \(y = f(x) = \frac{{x - 2}}{{x - 1}}\) a) Phương trình tiếp tuyến của (C) tại điểm M có tung độ bằng 4 là : \(y = 9x - 2\)
Đúng
Sai
b) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục hoành là\(y = x + 2\)
Đúng
Sai
c) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục tung là:\(y = x + 2\)
Đúng
Sai
d) Phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng \((d):y = - x + 1\) là \(y = - \frac{2}{5}x + 1\)
Đúng
Sai
Đáp án
a) Phương trình tiếp tuyến của (C) tại điểm M có tung độ bằng 4 là : \(y = 9x - 2\)
Đúng
Sai
b) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục hoành là\(y = x + 2\)
Đúng
Sai
c) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục tung là:\(y = x + 2\)
Đúng
Sai
d) Phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng \((d):y = - x + 1\) là \(y = - \frac{2}{5}x + 1\)
Đúng
Sai
Phương pháp giải :
Bước 1: Gọi M(x0; f(x0)) là tọa độ tiếp điểm của tiếp tuyến của (C) thì f'(x0) = k Bước 2: Giải phương trình f'(x0) = k với ẩn là x0. Bước 3: Phương trình tiếp tuyến của (C) có dạng y = k(x – x0) + f(x0) Lời giải chi tiết :
\(y' = f'(x) = \left( {\frac{{x - 2}}{{x - 1}}} \right)' = \frac{1}{{{{\left( {x - 1} \right)}^2}}}\) a) Gọi \(M({x_0};{y_0})\) là tiếp điểm. M có tung độ bằng 4 nên \(M(\frac{2}{3};4)\) Gọi k là hệ số góc của tiếp tuyển tại M nên \(k = f'\left( {\frac{2}{3}} \right) = 9\) Phương trình tiếp tuyến của (C) tại điểm \(M(\frac{2}{3};4)\) là \(y = 9(x - \frac{2}{3}) + 4\,\,hay\,\,y = 9x - 2\) b) Gọi \(M({x_0};{y_0})\) là tiếp điểm. M là giao của đồ thị với trục hoành nên \(M(2;0)\) Gọi k là hệ số góc của tiếp tuyến tại M nên \(k = f'\left( 2 \right) = 1\) Phương trình tiếp tuyến của (C) (C) tại điểm \(M(2;0)\) là \(\,y = x - 2\) c) Gọi \(M({x_0};{y_0})\) là tiếp điểm. M là giao điểm của đồ thị với trục tung nên \(M(0;2)\) Gọi k là hệ số góc của tiếp tuyến tại M. Khi đó \(k = f'\left( 0 \right) = 1\) Phương trình tiếp tuyến tại M là: \(\,y = (x - 0) + 2\,\,hay\,\,y = x + 2\) d) Gọi k là hệ số góc của tiếp tuyến của đồ thị (C) Do tiếp tuyến vuông góc với \((d):y = - x + 1\) nên \( - 1.k = - 1 \Leftrightarrow k = 1\) Gọi \(M({x_0},{y_0}) \in (C)\)mà tiếp tuyến của (C) tại M có hệ số góc k = 1 \(f'({x_0}) = 1 \Rightarrow \frac{1}{{{{(x - 1)}^2}}} = 1 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 2\\{x_0} = 0\end{array} \right.\) * Với \({x_0} = 2\) ta có \({y_0} = f(2) = 0 \Rightarrow {M_1}(2;0) \in (C)\) Phương trình tiếp tuyến của (C) tại \({M_1}(2;0)\)) là \(y = x - 2\) * Với \({x_0} = 0\) ta có \({y_0} = f(0) = 2 \Rightarrow {M_2}(0;2) \in (C)\) Phương trình tiếp tuyến của (C) tại \({M_2}(0;2)\) là \(\,y = x + 2\)
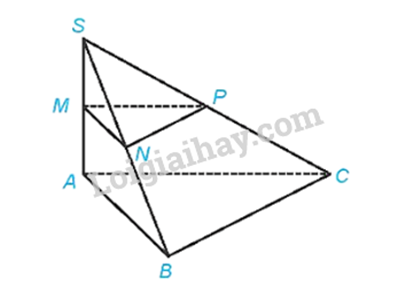
Câu 3 :
Cho hình chóp S.ABC có SA ⊥ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC. a) \(d((MNP),(ABC)) = h\)
Đúng
Sai
b) \(d(NP,(ABC)) = \frac{h}{2}\)
Đúng
Sai
c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
Đúng
Sai
d) \((MNP)//(ABC)\)
Đúng
Sai
Đáp án
a) \(d((MNP),(ABC)) = h\)
Đúng
Sai
b) \(d(NP,(ABC)) = \frac{h}{2}\)
Đúng
Sai
c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
Đúng
Sai
d) \((MNP)//(ABC)\)
Đúng
Sai
Phương pháp giải :
Sử dụng phương pháp tính khoảng cách từ điểm đến mặt phẳng và khoảng cách từ đường thẳng đến mặt phẳng Lời giải chi tiết :
a) Xét tam giác SAB có M là trung điểm của SA, N là trung điểm của SB nên MN là đường trung bình của tam giác SAB. Suy ra \(MN//AB\),do đó \(MN//(ABC)\) Xét tam giác SBC có N là trung điểm của SB, P là trung điểm của SC nên PN là đường trung bình của tam giác SBC. Suy ra \(PN//BC\),do đó \(PN//(ABC)\) Khi đó, \(d((MNP),(ABC)) = d(M,(ABC))\) Vì \(SA \bot (ABC)\) nên \(MA \bot (ABC)\). Do đó \(d(M,(ABC)) = MA\) Vì M là trung điểm SA nên \(AM = \frac{{SA}}{2} = \frac{h}{2}\) Do đó \(d((MNP),(ABC)) = \frac{h}{2}\) b) Vì \(PN//(ABC)\) nên \(d(NP,(ABC)) = d(N,(ABC))\) Vì \(MN//(ABC)\) nên \(d(N,(ABC)) = d(M,(ABC)) = MA = \frac{h}{2}\) Vậy \(d(N,(ABC)) = \frac{h}{2}\) c) Vì tam giác ABC là tam giác vuông tại B nên \(BC \bot AB\) Vì \(SA \bot (ABC)\) nên \(SA \bot BC\)mà \(BC \bot AB\) nên \(BC \bot (SAB)\), suy ra \((SBC) \bot (SAB)\) Kẻ \(AH \bot SB\) tại H Vì \(\left\{ \begin{array}{l}(SBC) \bot (SAB)\\(SBC) \cap (SAB) = SB\\AH \subset (SAB)\\AH \bot SB\end{array} \right. \Rightarrow AH \bot (SBC)\) Khi đó \(d(A,(SBC)) = AH\)\(\) Vì \(SA \bot (SBC)\) nên \(SA \bot AB\) Xét tam giác SAB vuông tại A, AH là đường cao, có: \(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{h^2}}} + \frac{1}{{{a^2}}} = \frac{{{a^2} + {h^2}}}{{{a^2}{h^2}}} \Rightarrow AH = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\) Vậy \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\) d)\(MN//(ABC)\) mà \(MN \subset (MNP) \Rightarrow (MNP)//(ABC)\)
Câu 4 :
Cho hàm số \(y = \sin x\) a) Đạo hàm của hàm số là \(y' = - cosx\)
Đúng
Sai
b) Biểu thức \(y'(\frac{\pi }{2}) = 0\)
Đúng
Sai
c) Biểu thức \(y''(\frac{\pi }{2}) = 0\)
Đúng
Sai
d) Biểu thức \({y^{(2024)}} = \sin (x + 1012\pi )\)
Đúng
Sai
Đáp án
a) Đạo hàm của hàm số là \(y' = - cosx\)
Đúng
Sai
b) Biểu thức \(y'(\frac{\pi }{2}) = 0\)
Đúng
Sai
c) Biểu thức \(y''(\frac{\pi }{2}) = 0\)
Đúng
Sai
d) Biểu thức \({y^{(2024)}} = \sin (x + 1012\pi )\)
Đúng
Sai
Phương pháp giải :
Sử dụng công thức tính đạo hàm của hàm số lượng giác Lời giải chi tiết :
a) \(y' = (\sin x)' = cosx\) b) \(y'(\frac{\pi }{2}) = \cos \frac{\pi }{2} = 0\) c) \(\begin{array}{l}y'' = \left( {cosx} \right)' = - \sin x\\y''\left( {\frac{\pi }{2}} \right) = - 1\end{array}\) d) \(\begin{array}{l}{y^{(n)}} = \sin (x + n\frac{\pi }{2})\\{y^{(2024)}} = \sin (x + 1012\pi )\end{array}\)
Phần III. Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6
Phương pháp giải :
Sử dụng phương pháp nhân liên hợp và phân tích thành nhân tử. Lời giải chi tiết :
\(\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {4x + 1} - 3}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {\sqrt {4x + 1} - 3} \right)\left( {\sqrt {4x + 1} + 3} \right)}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{(4x + 1) - 9}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}}\) \( = \mathop {\lim }\limits_{x \to 2} \frac{{4x - 8}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{4(x - 2)}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{4}{{\sqrt {4x + 1} + 3}} = \frac{4}{{\sqrt {4.2 + 1} + 3}} = \frac{2}{3}\). Phương pháp giải :
Sử dụng công thức tính đạo hàm của hàm hợp Lời giải chi tiết :
\(\begin{array}{l}y' = \left[ {{{\left( {{x^4} - 1} \right)}^4}} \right]' = 4.{\left( {{x^4} - 1} \right)^3}.4{x^3} = 16{x^3}{\left( {{x^4} - 1} \right)^3}\\y'(1) = 0\end{array}\) Phương pháp giải :
Bước 1: Tính \(f({x_0}) = {f_2}({x_0})\) Bước 2: Tính \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = \mathop {\lim }\limits_{x \to {x_0}} {f_1}(x) = L\) Bước 3: Nếu \({f_2}({x_0}) = L\) thì hàm số f(x) liên tục tại \({x_0}\) Nếu \({f_2}({x_0}) \ne L\)thì hàm số f(x) không liên tục tại \({x_0}\). (Đối với bài toán tìm tham số m để hàm số liên tục tại x0, ta thay bước 3 thành: Giải phương trình L = f2(x0), tìm m) Lời giải chi tiết :
Hàm số đã cho xác định trên R Ta có: \(f(1) = 1 - m\) \(\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 3x + 2}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)(x - 2)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} (x - 2) = - 1\) Để hàm số liên tục tại x = 1 khi \(f(1) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 3x + 2}}{{x - 1}} \Leftrightarrow 1 - m = - 1 \Leftrightarrow m = 2\) Phương pháp giải :
Sử dụng phương pháp tính góc giữa hai mặt phẳng Lời giải chi tiết :
\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AB\,\\BC \bot SA\,\,(Do\,\,SA \bot (ABCD))\\AB,SA \subset (SAB)\\AB \cap SA\end{array} \right. \Rightarrow BC \bot (SAB)\\ \Rightarrow BC \bot SB\end{array}\)\(SA \bot (ABCD) \Rightarrow SA \bot AB\) Ta có: \(\left\{ \begin{array}{l}(SBC) \cap (ABCD) = BC\\SB \subset (SBC),SB \bot BC\\AB \subset (ABCD),AB \bot BC\end{array} \right. \Rightarrow \left( {(SBC),(ABCD)} \right) = (SB,AB)\) Do \(SA \bot (ABCD) \Rightarrow SA \bot AB\). Xét tam giác SAB vuông tại A có: \(\tan (SB,AB) = \tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 2 }}{a} = \sqrt 2 \) Phương pháp giải :
Lập biểu thức tính khoảng cách từ điểm \(I( - 1;2)\) tới tiếp tuyển của đồ thị Sử dụng BĐT Cauchy để tìm giá trị lớn nhất của biểu thức Lời giải chi tiết :
Giả sử \(M({x_0};2 - \frac{3}{{{x_0} + 1}}) \in (C)\). PTTT của (C) tại M là: \(y = \frac{3}{{{{({x_0} + 1)}^2}}}(x - {x_0}) + 2 - \frac{3}{{{x_0} + 1}}\,\,\,(\Delta )\) Hay \(\begin{array}{l}(\Delta ):\,\,\,\frac{3}{{{{({x_0} + 1)}^2}}}x - y + \left[ {\frac{{3{x_0}}}{{{{({x_0} + 1)}^2}}} + 2 - \frac{3}{{{x_0} + 1}}} \right] = 0\,\,\,\\(\Delta ):\,\frac{3}{{{{({x_0} + 1)}^2}}}x - y + 2 - \frac{3}{{{{({x_0} + 1)}^2}}} = 0\\d(I,\Delta ) = \frac{{|\frac{3}{{{{({x_0} + 1)}^2}}}{x_0} - (2 - \frac{3}{{{x_0} + 1}}) + 2 - \frac{3}{{{{({x_0} + 1)}^2}}}|}}{{\sqrt {\frac{9}{{{{({x_0} + 1)}^4}}} + 1} }} = \frac{{6|{x_0} + 1|}}{{\sqrt {9 + {{({x_0} + 1)}^4}} }} = \frac{6}{{\sqrt {\frac{9}{{{{({x_0} + 1)}^2}}} + {{({x_0} + 1)}^2}} }}\end{array}\) Áp dụng BĐT Cauchy: \(\frac{9}{{{{({x_0} + 1)}^2}}} + {({x_0} + 1)^2} \ge 2\sqrt 9 = 6 \Rightarrow d \le \sqrt 6 \) Dấu “=” xảy ra khi \(\frac{9}{{{{({x_0} + 1)}^2}}} = {({x_0} + 1)^2} \Leftrightarrow {x_0} = - 1 \pm \sqrt 3 \) Vậy có hai điểm cần tìm là \(M( - 1 + \sqrt 3 ;2 - \sqrt 3 )\) hoặc \(M( - 1 - \sqrt 3 ;2 + \sqrt 3 )\) Phương pháp giải :
Lượng thức ăn mà trang trại ăn hết ở ngày thứ k là: \(M{(1 + r\% )^{k - 1}},k \in N*\) Trong đó: M: là lượng thứ ăn trang trại ăn hết trong mỗi ngày r (%): là % mức tiêu thụ thức ăn tăng thêm mỗi ngày Lời giải chi tiết :
Theo dự định, mỗi ngày, trang trại ăn hết: \(1:50 = \frac{1}{{50}}\)(lượng thức ăn) Lượng thức ăn mà trang trại ăn hết ở ngày thứ k là: \(\frac{1}{{50}}{(1 + 3\% )^{k - 1}},k \in N*\) Xác định số tự nhiên n nhỏ nhât để: \(\begin{array}{l}\frac{1}{{50}} + \frac{1}{{50}}(1 + 3\% ) + \frac{1}{{50}}{(1 + 3\% )^2} + ... + \frac{1}{{50}}{(1 + 3\% )^{n - 1}} \ge 1\\ \Leftrightarrow \frac{1}{{50}}(1 + 1,03 + 1,{03^2} + ... + 1,{03^{n - 1}}) \ge 1\\ \Leftrightarrow \frac{1}{{50}}.\frac{{1,{{03}^{n - 1}} - 1}}{{1,03 - 1}} \ge 1 \Leftrightarrow 1,{03^{n - 1}} - 1 \ge 1,5 \Leftrightarrow 1,{03^{n - 1}} \ge 2,5 \Leftrightarrow n - 1 \ge {\log _{1,03}}2,5 \Leftrightarrow n \ge 31,99 \Rightarrow {n_{Min}} = 32\end{array}\)
|