Nội dung từ Loigiaihay.Com
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng?
-
A.
\(AC \bot (SBD)\)
-
B.
\((SCD) \bot (SAD)\)
-
C.
\((SBD) \bot (SAC)\)
-
D.
\((SBC) \bot (SAC)\)
Sử dụng định lý đường thẳng vuông góc với mặt phẳng và hai mặt phẳng vuông góc với nhau
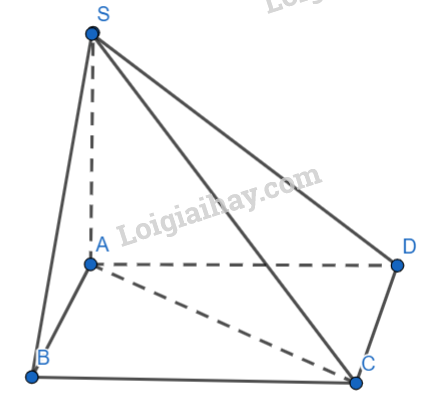
Ta có:
\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\,(do\,\,SA \bot (ABC{\rm{D}}))\\AD,SA \subset (SAD)\\AD \cap SA\end{array} \right. \Rightarrow CD \bot (SAD)\)
Mặt khác:
\(CD \subset (SCD) \Rightarrow (SCD) \bot (SAD)\)
Đáp án B.
Đáp án : B

Các bài tập cùng chuyên đề
Cho hàm số \(f(x) = \frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6.\) Phương trình \(f'(x) = 0\) có nghiệm là
Gọi (d) là tiếp tuyến của đồ thị hàm số\(y = f(x) = - {x^3} + x\) tại điểm \(M( - 2;6).\) Phương trình của (d) là
Tính \(\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1} - 2}}{{9 - {x^2}}}\) bằng
Cho \(u = u\left( x \right),v = v\left( x \right),v\left( x \right) \ne 0\); với k là hằng số. Hãy chọn khẳng định sai?
Đạo hàm của hàm số \(y = \frac{{2x - 1}}{{1 - x}}\) là
Cho hàm số: \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\quad khi\;x \ne 1\\m\quad \quad \quad khi\;x = 1\end{array} \right.\) . Để f(x) liên tục tại điểm \({x_0} = 1\)thì m bằng:
Tìm đạo hàm của hàm số sau \(y = {x^4} - 3{x^2} + 2x - 1\)
Cho hàm số \(f(x) = \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}},(a \in R,a \ne 0)\). Khi đó \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) bằng
Cho hình chóp \(S.ABC\) có đáy ABC là tam giác vuông tại B và SA vuông góc mặt đáy \(\left( {ABC} \right)\), \(SB = 2a\), \(AB = a\)( tham khảo hình vẽ). Tính góc giữa SB và \(mp\left( {ABC} \right)\)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Khẳng định nào sau đây đúng ?
Với hàm số \(g\left( x \right) = \frac{{\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{x - 1}};\,g'\left( 2 \right)\) bằng
Tính giới hạn: \(\mathop {lim}\limits_{x \to 2} \frac{{\sqrt {4x + 1} - 3}}{{x - 2}}\).
Cho hàm số: \(y = {\left( {{x^4} - 1} \right)^4}\). Tính \(y'(1)\)
Tìm m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 3x + 2}}{{x - 1}}\,\,\,\;khi\,\,x \ne 1\\1 - mx\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 1\end{array} \right.\)liên tục tại điểm\({x_0} = 1\)
Cho hình chóp S.ABCD đáy là hình vuông cạnh a , cạnh bên SA \( \bot \)(ABCD) và
SA = a\(\sqrt 2 \). Tính tan của góc giữa hai mp (SBC) và (ABCD).
Cho hàm số \(y = \frac{{2x - 1}}{{x + 1}}\). Tìm tọa độ điểm M thuộc đồ thị sao cho khoảng cách từ điểm \(I( - 1;2)\)tới tiếp tuyến của đồ thị tại M là lớn nhất.
Với mức tiêu thụ thức ăn cho cá hàng ngày của hộ gia đình A không đổi như dự định thì lượng thức ăn dự trữ sẽ hết sau 50 ngày. Nhưng trên thực tế, mức tiêu thụ thức ăn tăng thêm 3% từ ngày đầu tiên và cứ tiếp tục như vậy, ngày sau tăng thêm 3% so với ngày kề trước đó. Hỏi thực tế, lượng thức ăn dự trữ đó sẽ hết sau bao nhiêu ngày? (làm tròn đến hàng đơn vị).












