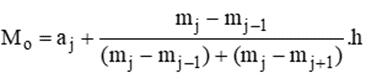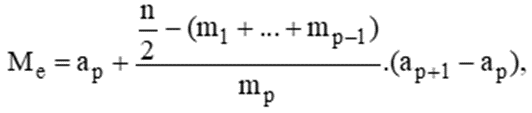Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 8Phần trắc nghiệmĐề bài
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Góc có số đo \(\frac{\pi }{6}\) radian bằng bao nhiêu độ?
Câu 2 :
Cho \(\cos \alpha = - \frac{1}{4}\) với \(\pi < \alpha < \frac{{3\pi }}{2}\). Giá trị của \(\sin \alpha \) là?
Câu 3 :
Giá trị lượng giác \(\cos \left( {\frac{{37\pi }}{{12}}} \right)\) bằng?
Câu 4 :
Hàm số nào sau đây là hàm số chẵn?
Câu 5 :
Nghiệm của phương trình \(\cos x = 0\) là?
Câu 6 :
Số hạng thứ 3 của dãy số \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_n} = 2{u_{n - 1}} + 3}\end{array}} \right.\) là?
Câu 7 :
Dãy số nào sau đây là cấp số cộng?
Câu 8 :
Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 12\) và công bội \(q = - 2\). Số hạng thứ sáu của cấp số nhân đã cho bằng
Câu 9 :
Số lượng khách hàng nữ mua bảo hiểm nhân thọ trong một ngày được thống kê trong bảng tần số ghép nhóm sau:
Giá trị đại diện của nhóm [30;40) là
Câu 10 :
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng).
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng sau đây?
Câu 11 :
Số nghiệm của phương trình \(\sin 2x + \cos x = 0\) trên \([0;2\pi ]\) là
Câu 12 :
Cho cấp số cộng \(({u_n})\) có \({u_5} = - 10\) và \({u_{15}} = 60\). Tổng 20 số hạng đầu tiên của cấp số cộng là
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Cho phương trình lượng giác \(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0\). Khi đó a) Phương trình tương đương \(\sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \frac{\pi }{3}\)
Đúng
Sai
b) Phương trình có nghiệm là \(x = \frac{\pi }{4} + k2\pi \); \(x = \frac{{7\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\)
Đúng
Sai
c) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{\pi }{4}\)
Đúng
Sai
d) Số nghiệm của phương trình trong khoảng \(( - \pi ;\pi )\) là hai nghiệm
Đúng
Sai
Câu 2 :
Cho \(\cos \alpha = - \frac{1}{4}\) và \(\pi < \alpha < \frac{{3\pi }}{2}\). Khi đó a) \({\sin ^2}\alpha = \frac{{15}}{{16}}\)
Đúng
Sai
b) \(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
Đúng
Sai
c) \(\tan \alpha = \sqrt {15} \)
Đúng
Sai
d) \(\cot \alpha = - \frac{1}{{\sqrt {15} }}\)
Đúng
Sai
Câu 3 :
Cho dãy số \(({u_n})\) biết \({u_n} = {2^n} + 1\). Khi đó a) Dãy số \(({u_n})\) là dãy số tăng
Đúng
Sai
b) Dãy số \(({u_n})\) là dãy số bị chặn
Đúng
Sai
c) \({u_6} = 65\)
Đúng
Sai
d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\)
Đúng
Sai
a) Giá trị đại diện của nhóm [150;155) bằng 152,5
Đúng
Sai
b) Nhóm chứa mốt của mẫu số liệu ở lô hàng A là [155;160)
Đúng
Sai
c) Nhóm chứa mốt của mẫu số liệu ở lô hàng B là [160;165)
Đúng
Sai
d) Theo số trung bình thì cam ở lô hàng B nặng hơn cam ở lô hàng A
Đúng
Sai
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
Hằng ngày mực nước tại một cảng biển lên xuống theo thủy triều. Độ sâu h (m) của mực nước theo thời gian t (giờ) trong một ngày được cho bởi công thức \(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) với \(0 \le t \le 24\). Tính thời điểm mực nước tại cảng cao nhất. Đáp án:
Câu 2 :
Phương trình \(2\sin 2x + 4\cos x = 0\) có bao nhiêu nghiệm trong khoảng (0;3000)? Đáp án:
Câu 3 :
Công ty cây xanh X trồng 496 cây hoa trong một khu vườn hình tam giác như sau: hàng thứ nhất trồng 1 cây hoa, kể từ hàng thứ hai trở đi số cây hoa trồng mỗi hàng nhiều hơn 1 cây so với hàng liền trước nó. Hỏi công ty cây xanh X trồng được bao nhiêu hàng cây trong khu vườn hình tam giác đó. Đáp án:
Câu 4 :
Cho dãy số \(({u_n})\) biết \({u_n} = n + \frac{1}{n}\). Tìm m để dãy số \(({u_n})\) bị chặn dưới bởi m. Đáp án:
Câu 5 :
Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 11A.
Số học sinh có chiều cao bao nhiêu cm là nhiều nhất (làm tròn đến hàng đơn vị)? Đáp án:
Câu 6 :
Trong một hội thao, thời gian chạy 200 m của một nhóm vận động viên được ghi lại trong bảng sau:
Dựa vào bảng dữ liệu trên, ban tổ chức muốn chọn ra khoảng 50% số vận động viên chạy nhanh nhất để tiếp tục thi vòng 2. Ban tổ chức nên chọn các vận động viên có thời gian chạy không quá bao nhiêu giây (kết quả làm tròn đến hàng phần mười)? Đáp án: Lời giải và đáp án
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Góc có số đo \(\frac{\pi }{6}\) radian bằng bao nhiêu độ?
Đáp án : A Phương pháp giải :
Áp dụng quan hệ giữa radian và độ: \(1rad = {\left( {\frac{{180}}{\pi }} \right)^o}\), \({1^o} = \frac{\pi }{{180}}rad\). Lời giải chi tiết :
Ta có: \(\frac{\pi }{6}rad = \frac{\pi }{6}.\frac{{{{180}^o}}}{\pi } = {30^o}\).
Câu 2 :
Cho \(\cos \alpha = - \frac{1}{4}\) với \(\pi < \alpha < \frac{{3\pi }}{2}\). Giá trị của \(\sin \alpha \) là?
Đáp án : B Phương pháp giải :
Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) và sử dụng đường tròn lượng giác để xét dấu. Lời giải chi tiết :
Ta có: \({\sin ^2}\alpha = 1 - {\cos ^2}\alpha = 1 - {\left( {\frac{1}{4}} \right)^2} = \frac{{15}}{{16}}\), suy ra \(\sin \alpha = \pm \frac{{\sqrt {15} }}{4}\). Vì \(\pi < \alpha < \frac{{3\pi }}{2}\) nên điểm cuối của cung \(\alpha \) thuộc cung phần tư thứ III, do đó \(\sin \alpha < 0\). Vậy \(\sin \alpha = - \frac{{\sqrt {15} }}{4}\).
Câu 3 :
Giá trị lượng giác \(\cos \left( {\frac{{37\pi }}{{12}}} \right)\) bằng?
Đáp án : C Phương pháp giải :
Sử dụng công thức cộng lượng giác \(\cos (a - b) = \cos a.\cos b + \sin b.\sin a\). Lời giải chi tiết :
\(\cos \frac{{37\pi }}{{12}} = \cos \left( {3\pi + \frac{\pi }{{12}}} \right) = \cos \left( {\pi + \frac{\pi }{{12}}} \right) = - \cos \frac{\pi }{{12}} = - \cos \left( {\frac{\pi }{3} - \frac{\pi }{4}} \right)\) \( = - \left( {\cos \frac{\pi }{3}.\cos \frac{\pi }{4} + \sin \frac{\pi }{3}.\sin \frac{\pi }{4}} \right) = - \frac{{\sqrt 6 + \sqrt 2 }}{4}\).
Câu 4 :
Hàm số nào sau đây là hàm số chẵn?
Đáp án : A Phương pháp giải :
Cho hàm số y = f(x) liên tục và xác định trên khoảng (đoạn) K. Với mỗi \(x \in K\) thì \( - x \in K\). - Nếu f(x) = f(-x) thì hàm số y = f(x) là hàm số chẵn trên tập xác định. - Nếu f(-x) = -f(x) thì hàm số y = f(x) là hàm số lẻ trên tập xác định. Lời giải chi tiết :
Xét phương án A, hàm số \(y = \left| {\sin x} \right|\) có tập xác định D = R, suy ra có \(x \in R\) thì \( - x \in R\). Mặt khác, \(f( - x) = \left| {\sin ( - x)} \right| = \left| { - \sin x} \right| = \sin x = f(x)\). Vậy hàm số đáp án A là hàm số chẵn.
Câu 5 :
Nghiệm của phương trình \(\cos x = 0\) là?
Đáp án : C Phương pháp giải :
Nghiệm của phương trình lượng giác cơ bản. Lời giải chi tiết :
\(\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
Câu 6 :
Số hạng thứ 3 của dãy số \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_n} = 2{u_{n - 1}} + 3}\end{array}} \right.\) là?
Đáp án : D Phương pháp giải :
Tìm lần lượt \({u_2},{u_3}\) bằng cách thay n vào công thức tổng quát. Lời giải chi tiết :
Ta có: \({u_2} = 2{u_{2 - 1}} + 3 = 2{u_1} + 3 = 2.1 + 3 = 5\) \({u_3} = 2{u_{3 - 1}} + 3 = 2{u_2} + 3 = 2.5 + 3 = 13\)
Câu 7 :
Dãy số nào sau đây là cấp số cộng?
Đáp án : C Phương pháp giải :
Dãy số lập thành một cấp số cộng khi và chỉ khi hai phần tử liên tiếp sai khác nhau một hằng số. Lời giải chi tiết :
Xét hiệu các phần tử liên tiếp trong các dãy số, chỉ có dãy ở đáp án C phần tử sau hơn phần tử liền trước 2 đơn vị (8 – 6 = 6 – 4 = 4 – 2 = 2 – 0 = 2).
Câu 8 :
Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 12\) và công bội \(q = - 2\). Số hạng thứ sáu của cấp số nhân đã cho bằng
Đáp án : B Phương pháp giải :
Sử dụng công thức \({u_n} = {u_1}{q^{n - 1}}\). Lời giải chi tiết :
Ta có: \({u_6} = {u_1}{q^{6 - 1}} = 12.{( - 2)^5} = - 384\).
Câu 9 :
Số lượng khách hàng nữ mua bảo hiểm nhân thọ trong một ngày được thống kê trong bảng tần số ghép nhóm sau:
Giá trị đại diện của nhóm [30;40) là
Đáp án : C Phương pháp giải :
Giá trị đại diện nhóm \([{a_m};{a_n})\) là: \(\frac{{{a_m} + {a_n}}}{2}\). Lời giải chi tiết :
Ta có giá trị đại diện nhóm [30;40) là: \(\frac{{30 + 40}}{2} = 35\).
Câu 10 :
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng).
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng sau đây?
Đáp án : B Phương pháp giải :
Tính số trung bình của mẫu số liệu trên. Lời giải chi tiết :
Ta có bảng sau:
Khi đó \(\overline x = \frac{{2.6 + 7.8 + 7.10 + 3.12 + 1.14}}{{20}} = 9,4\).
Câu 11 :
Số nghiệm của phương trình \(\sin 2x + \cos x = 0\) trên \([0;2\pi ]\) là
Đáp án : D Phương pháp giải :
Biến đổi phương trình trở thành dạng phương trình tích, đưa về giải phương trình lượng giác cơ bản. Lời giải chi tiết :
\(\sin 2x + \cos x = 0 \Leftrightarrow 2\sin x.\cos x + \cos x = 0 \Leftrightarrow \cos x.(2\sin x + 1) = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos x = 0}\\{2\sin x + 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos x = 0}\\{\sin x = - \frac{1}{2}}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{2} + k\pi }\\{x = - \frac{\pi }{6} + k2\pi }\\{x = \frac{{7\pi }}{6} + k2\pi }\end{array}} \right.} \right.\) với \(k \in \mathbb{Z}\). Vì \(x \in [0;2\pi ]\) nên chỉ có 4 nghiệm thỏa mãn: \(x = \left\{ {\frac{\pi }{2};\frac{{3\pi }}{2};\frac{{7\pi }}{6};\frac{{11\pi }}{6}} \right\}\).
Câu 12 :
Cho cấp số cộng \(({u_n})\) có \({u_5} = - 10\) và \({u_{15}} = 60\). Tổng 20 số hạng đầu tiên của cấp số cộng là
Đáp án : C Phương pháp giải :
Tìm số hạng đầu và công sai dựa theo công thức \({u_n} = {u_1} + (n - 1)d\). Từ đó tìm tổng 20 số hạng đầu tiên \({S_n} = \frac{{({u_1} + {u_n})n}}{2}\). Lời giải chi tiết :
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{{u_5} = {u_1} + 4d}\\{{u_{15}} = {u_1} + 14d}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 10 = {u_1} + 4d}\\{60 = {u_1} + 14d}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{u_1} = - 38}\\{d = 7}\end{array}} \right.\) Từ đó ta tính được \({u_{20}} = - 38 + (20 - 1)7 = 95\). Vậy tổng 20 số hạng đầu của cấp số cộng là \({S_{20}} = \frac{{({u_1} + {u_{20}}).20}}{2} = \frac{{( - 38 + 95).20}}{2} = 570\).
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Cho phương trình lượng giác \(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0\). Khi đó a) Phương trình tương đương \(\sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \frac{\pi }{3}\)
Đúng
Sai
b) Phương trình có nghiệm là \(x = \frac{\pi }{4} + k2\pi \); \(x = \frac{{7\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\)
Đúng
Sai
c) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{\pi }{4}\)
Đúng
Sai
d) Số nghiệm của phương trình trong khoảng \(( - \pi ;\pi )\) là hai nghiệm
Đúng
Sai
Đáp án
a) Phương trình tương đương \(\sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \frac{\pi }{3}\)
Đúng
Sai
b) Phương trình có nghiệm là \(x = \frac{\pi }{4} + k2\pi \); \(x = \frac{{7\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\)
Đúng
Sai
c) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{\pi }{4}\)
Đúng
Sai
d) Số nghiệm của phương trình trong khoảng \(( - \pi ;\pi )\) là hai nghiệm
Đúng
Sai
Phương pháp giải :
Giải phương trình lượng giác \(\sin x = a\): - Nếu \(\left| a \right| > 1\) thì phương trình vô nghiệm. - Nếu \(\left| a \right| \le 1\) thì chọn cung \(\alpha \) sao cho \(\sin \alpha = a\). Khi đó phương trình trở thành: \(\sin x = \sin \alpha \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha + k2\pi }\\{x = \pi - \alpha + k2\pi }\end{array}} \right.\) với \(k \in \mathbb{Z}\). Lời giải chi tiết :
\(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0 \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = - \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x - \frac{\pi }{{12}} = - \frac{\pi }{3} + k2\pi }\\{x - \frac{\pi }{{12}} = \pi + \frac{\pi }{3} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - \frac{\pi }{4} + k2\pi }\\{x = \frac{{17\pi }}{{12}} + k2\pi }\end{array}} \right.\) a) Sai. \(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0 \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = - \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\) b) Sai. Phương trình có nghiệm là \(x = - \frac{\pi }{4} + k2\pi \); \(x = \frac{{17\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\). c) Đúng. + Xét họ nghiệm \(x = - \frac{\pi }{4} + k2\pi \): Nghiệm âm lớn nhất là \(x = - \frac{\pi }{4}\) khi k = 0. + Xét họ nghiệm \(x = \frac{{17\pi }}{{12}} + k2\pi \): Nghiệm âm lớn nhất là \(x = - \frac{{7\pi }}{{12}}\) khi k = -1. Vì \( - \frac{\pi }{4} > - \frac{{7\pi }}{{12}}\) nên nghiệm âm lớn nhất là \(x = - \frac{\pi }{4}\). d) Đúng. + Xét họ nghiệm \(x = - \frac{\pi }{4} + k2\pi \): \( - \pi < x < \pi \Leftrightarrow - \pi < - \frac{\pi }{4} + k2\pi < \pi \) \( \Leftrightarrow - 1 < - \frac{1}{4} + 2k < 1 \Leftrightarrow - \frac{3}{4} < 2k < \frac{5}{4} \Leftrightarrow - \frac{3}{8} < k < \frac{5}{8}\). Vậy chỉ có k = 0 thỏa mãn. Khi đó \(x = - \frac{\pi }{4}\). + Xét họ nghiệm \(x = \frac{{17\pi }}{{12}} + k2\pi \): \( - \pi < x < \pi \Leftrightarrow - \pi < \frac{{17\pi }}{{12}} + k2\pi < \pi \Leftrightarrow - 1 < \frac{{17}}{{12}} + 2k < 1\) \( \Leftrightarrow - \frac{{29}}{{12}} < 2k < - \frac{5}{{12}} \Leftrightarrow - \frac{{29}}{{24}} < k < - \frac{5}{{24}}\). Vậy chỉ có k = -1 thỏa mãn. Khi đó \(x = - \frac{{7\pi }}{{12}}\). Vậy phương trình có hai nghiệm thuộc khoảng \(( - \pi ;\pi )\) là \(x = - \frac{\pi }{4}\) và \(x = - \frac{{7\pi }}{{12}}\).
Câu 2 :
Cho \(\cos \alpha = - \frac{1}{4}\) và \(\pi < \alpha < \frac{{3\pi }}{2}\). Khi đó a) \({\sin ^2}\alpha = \frac{{15}}{{16}}\)
Đúng
Sai
b) \(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
Đúng
Sai
c) \(\tan \alpha = \sqrt {15} \)
Đúng
Sai
d) \(\cot \alpha = - \frac{1}{{\sqrt {15} }}\)
Đúng
Sai
Đáp án
a) \({\sin ^2}\alpha = \frac{{15}}{{16}}\)
Đúng
Sai
b) \(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
Đúng
Sai
c) \(\tan \alpha = \sqrt {15} \)
Đúng
Sai
d) \(\cot \alpha = - \frac{1}{{\sqrt {15} }}\)
Đúng
Sai
Phương pháp giải :
a) Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) và dựa vào góc phần tư của đường tròn lượng giác để xét dấu. b) Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) và dựa vào góc phần tư của đường tròn lượng giác để xét dấu. c) \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{1}{{\cot \alpha }}\) d) \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{1}{{\tan \alpha }}\) Lời giải chi tiết :
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( { - \frac{1}{4}} \right)^2} = \frac{{15}}{{16}} \Rightarrow \sin \alpha = \pm \frac{{\sqrt {15} }}{4}\). Vì \(\pi < \alpha < \frac{{3\pi }}{2}\) nên điểm cuối của cung \(\alpha \) thuộc góc phần tư thứ III nên \(\sin \alpha < 0\). Vậy \(\sin \alpha = - \frac{{\sqrt {15} }}{4}\). \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{ - \frac{1}{4}}}{{ - \frac{{\sqrt {15} }}{4}}} = \sqrt {15} \); \(\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{1}{{\sqrt {15} }}\). a) Đúng. b) Sai. c) Đúng. d) Sai.
Câu 3 :
Cho dãy số \(({u_n})\) biết \({u_n} = {2^n} + 1\). Khi đó a) Dãy số \(({u_n})\) là dãy số tăng
Đúng
Sai
b) Dãy số \(({u_n})\) là dãy số bị chặn
Đúng
Sai
c) \({u_6} = 65\)
Đúng
Sai
d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\)
Đúng
Sai
Đáp án
a) Dãy số \(({u_n})\) là dãy số tăng
Đúng
Sai
b) Dãy số \(({u_n})\) là dãy số bị chặn
Đúng
Sai
c) \({u_6} = 65\)
Đúng
Sai
d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\)
Đúng
Sai
Phương pháp giải :
a) Dãy số \(({u_n})\) là dãy số giảm nếu \({u_n} > {u_{n + 1}}\). Dãy số \(({u_n})\) là dãy số tăng nếu \({u_n} < {u_{n + 1}}\). b) Dãy số \(({u_n})\) là dãy số bị chặn nếu \(({u_n})\) vừa bị chặn trên vừa bị chặn dưới, tức tồn tại hai số m, M sao cho \(m \le {u_n} \le M\) \(\forall n \in \mathbb{N}*\). c) Tính \({u_6}\) bằng công thức \({u_n} = {2^n} + 1\). d) Thay n + 2 vào n trong công thức số hạng tổng quát \({u_n} = {2^n} + 1\). Lời giải chi tiết :
a) Đúng. \({u_{n + 1}} - {u_n} = {2^{n + 1}} + 1 - ({2^n} + 1) = {2^{n + 1}} - {2^n} = {2^n}(2 - 1) = {2^n} > 0\) với mọi n. Vậy dãy số là dãy tăng. b) Sai. Dãy không bị chặn trên vì không có giá trị M nào để \({2^n} < M\) với mọi n. Vậy dãy số không bị chặn. c) Đúng. \({u_6} = {2^6} + 1 = 64 + 1 = 65\). d) Sai. \({u_{n + 2}} = {2^{n + 2}} + 1 = {4.2^n} + 1\). a) Giá trị đại diện của nhóm [150;155) bằng 152,5
Đúng
Sai
b) Nhóm chứa mốt của mẫu số liệu ở lô hàng A là [155;160)
Đúng
Sai
c) Nhóm chứa mốt của mẫu số liệu ở lô hàng B là [160;165)
Đúng
Sai
d) Theo số trung bình thì cam ở lô hàng B nặng hơn cam ở lô hàng A
Đúng
Sai
Đáp án
a) Giá trị đại diện của nhóm [150;155) bằng 152,5
Đúng
Sai
b) Nhóm chứa mốt của mẫu số liệu ở lô hàng A là [155;160)
Đúng
Sai
c) Nhóm chứa mốt của mẫu số liệu ở lô hàng B là [160;165)
Đúng
Sai
d) Theo số trung bình thì cam ở lô hàng B nặng hơn cam ở lô hàng A
Đúng
Sai
Phương pháp giải :
a) Giá trị đại diện nhóm \([{a_m};{a_n})\) là: \(\frac{{{a_m} + {a_n}}}{2}\). b) Nhóm chứa mốt có tần số cao nhất. c) Nhóm chứa mốt có tần số cao nhất. d) Tính cân nặng trung bình của mỗi lô hàng rồi so sánh. Lời giải chi tiết :
a) Đúng. Giá trị đại diện nhóm [150;155) là \(\frac{{150 + 155}}{2} = 152,5\). b) Sai. Nhóm chứa mốt của mẫu số liệu ở lô hàng A là [160;165) vì có tần số cao nhất là 12. c) Sai. Nhóm chứa mốt của mẫu số liệu ở lô hàng B là [165;170) vì có tần số cao nhất là 10. d) Đúng. Bảng thống kê số lượng cam theo giá trị đại diện:
Cân nặng trung bình của mỗi quả cam ở lô A là: \(\overline {{x_A}} = \frac{{152,5.2 + 157,5.6 + 162,5.12 + 167,5.4 + 172,5.1}}{{25}} = 161,7\) (gam). Cân nặng trung bình của mỗi quả cam ở lô B là: \(\overline {{x_B}} = \frac{{152,5.1 + 157,5.3 + 162,5.7 + 167,5.10 + 172,5.4}}{{25}} = 165,1\) (gam). Thấy \(\overline {{x_A}} < \overline {{x_B}} \). Vậy nếu so sánh theo số trung bình thì cam ở lô hàng B nặng hơn cam ở lô hàng A.
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
Hằng ngày mực nước tại một cảng biển lên xuống theo thủy triều. Độ sâu h (m) của mực nước theo thời gian t (giờ) trong một ngày được cho bởi công thức \(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) với \(0 \le t \le 24\). Tính thời điểm mực nước tại cảng cao nhất. Đáp án: Đáp án
Đáp án: Phương pháp giải :
Tìm t sao cho hàm số \(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) đạt giá trị lớn nhất. Lời giải chi tiết :
\(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) đạt giá trị lớn nhất khi \(\sin \left( {\frac{\pi }{{12}}t} \right) = 1 \Leftrightarrow \frac{\pi }{{12}}t = \frac{\pi }{2} + k2\pi \Leftrightarrow t = 6 + 24k\) (giờ). Vì \(0 \le t \le 24\) nên chỉ có giá trị t = 6 thỏa mãn. Vậy thời điểm mực nước tại cảng cao nhất là lúc 6 giờ.
Câu 2 :
Phương trình \(2\sin 2x + 4\cos x = 0\) có bao nhiêu nghiệm trong khoảng (0;3000)? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Giải phương trình lượng giác bằng cách biến đổi về dạng phương trình tích. Xét họ nghiệm trong khoảng (0;3000) để tìm số giá trị k nguyên thỏa mãn. Lời giải chi tiết :
Ta có: \(2\sin 2x + 4\cos x = 0 \Rightarrow 4\sin x.\cos x + 4\cos x = 0 \Rightarrow 4\cos x.(\sin x + 1) = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos x = 0}\\{\sin x = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{2} + k\pi }\\{x = \frac{{3\pi }}{2} + k2\pi }\end{array}} \right. \Leftrightarrow x = \frac{\pi }{2} + k\pi \) với \(k \in \mathbb{Z}\). Xét họ nghiệm \(x = \frac{\pi }{2} + k\pi \), ta có: \(0 < \frac{\pi }{2} + k\pi < 3000 \Leftrightarrow - \frac{\pi }{2} < k\pi < 3000 - \frac{\pi }{2} \Leftrightarrow - \frac{1}{2} < k < \frac{{3000}}{\pi } - \frac{1}{2} \Leftrightarrow - 0,5 < k < 954,43\). Mà \(k \in \mathbb{Z}\) nên \(k \in \{ 0;1;2;3;...;954\} \), tức có 955 giá trị k thỏa mãn. Vậy phương trình có 955 nghiệm thuộc khoảng (0;3000).
Câu 3 :
Công ty cây xanh X trồng 496 cây hoa trong một khu vườn hình tam giác như sau: hàng thứ nhất trồng 1 cây hoa, kể từ hàng thứ hai trở đi số cây hoa trồng mỗi hàng nhiều hơn 1 cây so với hàng liền trước nó. Hỏi công ty cây xanh X trồng được bao nhiêu hàng cây trong khu vườn hình tam giác đó. Đáp án: Đáp án
Đáp án: Phương pháp giải :
Số cây mỗi hàng lập thành một cấp số cộng với tổng n số hạng là 496, số hạng đầu \({u_1} = 1\) công sai d = 1. Tìm n. Lời giải chi tiết :
Số cây mỗi hàng lập thành một cấp số cộng với tổng n số hạng là 496, số hạng đầu \({u_1} = 1\) công sai d = 1. Ta có: \(496 = \frac{{2.1 + (n - 1).1}}{2}.n \Leftrightarrow 992 = (2 + n - 1).n = {n^2} + n - 992 = 0\). Ta tính được n = 31 hoặc n = -32 (loại). Vậy số hàng cây trồng được là 31 hàng.
Câu 4 :
Cho dãy số \(({u_n})\) biết \({u_n} = n + \frac{1}{n}\). Tìm m để dãy số \(({u_n})\) bị chặn dưới bởi m. Đáp án: Đáp án
Đáp án: Phương pháp giải :
Chứng minh dãy số tăng và bị chặn dưới tại \(m = {u_1}\). Lời giải chi tiết :
Xét \({u_{n + 1}} - {u_n} = \left( {n + 1 + \frac{1}{{n + 1}}} \right) - \left( {n + \frac{1}{n}} \right) = 1 + \frac{1}{{n + 1}} - \frac{1}{n} = \left( {1 - \frac{1}{n}} \right) + \frac{1}{{n + 1}}\). Ta có: \(n \ge 1 \Leftrightarrow \frac{1}{n} < 1 \Leftrightarrow 1 - \frac{1}{n} > 0\); \(n \ge 1 \Rightarrow \frac{1}{{n + 1}} > 0\). Vậy \({u_{n + 1}} - {u_n} > 0\), tức dãy số tăng. Khi đó, dãy bị chặn dưới bởi \({u_1} = 1 + \frac{1}{1} = 2 = m\).
Câu 5 :
Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 11A.
Số học sinh có chiều cao bao nhiêu cm là nhiều nhất (làm tròn đến hàng đơn vị)? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Tìm mốt của mẫu số liệu. Bước 1: Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm j: [aj; aj+1). Bước 2: Mốt được xác định là
trong đó mj là tần số của nhóm j (quy ước mo = mk+1 = 0) và h là độ dài của nhóm. Lời giải chi tiết :
Tần số lớn nhất là 14 nên nhóm chứa mốt là nhóm [150;155). Ta có \({M_o} = 150 + \frac{{14 - 7}}{{(14 - 7) + (14 - 10)}}(155 - 150) \approx 153\). Vậy số học sinh có chiều cao khoảng 153 cm là nhiều nhất.
Câu 6 :
Trong một hội thao, thời gian chạy 200 m của một nhóm vận động viên được ghi lại trong bảng sau:
Dựa vào bảng dữ liệu trên, ban tổ chức muốn chọn ra khoảng 50% số vận động viên chạy nhanh nhất để tiếp tục thi vòng 2. Ban tổ chức nên chọn các vận động viên có thời gian chạy không quá bao nhiêu giây (kết quả làm tròn đến hàng phần mười)? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Tìm trung vị của mẫu số liệu trên. Bước 1: Xác định nhóm chứa trung vị. Giả sử đó là nhóm thứ p: [ap; ap+1). Bước 2: Trung vị
trong đó n là cỡ mẫu, mp là tần số nhóm p. Với p = 1, ta quy ước m1 + ….+ mp-1 = 0. Lời giải chi tiết :
Cỡ mẫu là n = 5 + 12 +32 + 45 + 30 = 124. Gọi \({x_1};{x_2};...;{x_{124}}\) là thời gian chạy của 124 vận động viên tham gia hội thao và giả sử dãy này được sắp xếp theo thứ tự tăng dần. Khi đó, trung vị là \(\frac{{{x_{62}} + {x_{63}}}}{2}\). Do giá trị \({x_{62}},{x_{63}}\) thuộc nhóm [22,5;23) nên nhóm này chứa trung vị. Trung vị là \({M_e} = 22,5 + \frac{{\frac{{124}}{2} - (5 + 12 + 32)}}{{45}}.(23 - 22,5) \approx 22,6\). Vậy ban tổ chức nên chọn vận động viên có thời gian chạy không quá 22,6 giây.
|