Đề thi học kì 1 Toán 8 - Đề số 4 - Cánh diềuTổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên Phần trắc nghiệm (3 điểm) Câu 1: Kết quả thương của phép chia (left( 3x{{y}^{2}}-2{{x}^{2}}y+{{x}^{3}} right):left( -frac{1}{2}x right)) là :Đề bài
I. Trắc nghiệm
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1 :
Kết quả thương của phép chia \(\left( {3x{y^2} - 2{x^2}y + {x^3}} \right):\left( { - \frac{1}{2}x} \right)\) là:
Câu 2 :
Giá trị của đa thức \({x^3}y - 14{y^3} - 6x{y^2} + y + 2\) tại x = -1 ; y = 0,5 là:
Câu 3 :
Phân thức \(\frac{2}{{x - 3}}\) không có nghĩa khi:
Câu 4 :
Phân thức nghịch đảo của phân thức \(\frac{2}{{x - 4}}\left( {x \ne 4} \right)\) là:
Câu 5 :
Rút gọn phân thức \(\frac{{x - 3}}{{{x^2} - 9}}\left( {x \ne \pm 3} \right)\), ta được kết quả:
Câu 6 :
Hai đường chéo của hình chữ nhật
Câu 7 :
Một tứ giác là hình bình hành nếu nó là:
Câu 8 :
Những tứ giác nào sau đây có hai đường chéo bằng nhau?
Câu 9 :
Độ dài một cạnh góc vuông và cạnh huyền của một tam giác vuông lần lượt là 3cm và 5cm. Diện tích của tam giác vuông đó là:
Câu 10 :
Cho hình khối chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 2a. Tính thể tích V của khối chóp S.ABC.
Câu 11 :
Một hình chóp tứ giác đều S.ABCD có độ dài trung đoạn là 12cm và đáy là hình vuông có chu vi là 40cm. Diện tích xung quanh của hình chóp tứ giác đều đó là:
Câu 12 :
Nhà bác học Galileo Galilei (1564 – 1642) là người đầu tiên phát hiện ra quan hệ giữa quãng đường chuyển động y (m) và thời gian chuyển động x (giây) của một vật được biểu diễn gần đúng bởi hàm số \(y = 5{x^2}\). Quãng đường mà vật đó chuyển động được sau 3 giây là :
Câu 14 :
Xác định đường thẳng \(y = ax + b;(a \ne 0)\) có hệ số góc bằng 2 và đi qua điểm A (2;1)
Câu 15 :
“Trên mặt phẳng, ta vẽ hai trục số Ox, Oy …… với nhau và ……. tại gốc tọa độ O của mỗi trục. Khi đó ta có hệ trục tọa độ Oxy”. Các từ lần lượt cần điền đó là :
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1 :
Kết quả thương của phép chia \(\left( {3x{y^2} - 2{x^2}y + {x^3}} \right):\left( { - \frac{1}{2}x} \right)\) là:
Đáp án : C Phương pháp giải :
Sử dụng quy tắc chia đa thức cho đơn thức. Lời giải chi tiết :
Ta có: \(\begin{array}{l}\left( {3x{y^2} - 2{x^2}y + {x^3}} \right):\left( { - \frac{1}{2}x} \right)\\ = 3x{y^2}:\left( { - \frac{1}{2}x} \right) - 2{x^2}y:\left( { - \frac{1}{2}x} \right) + {x^3}:\left( { - \frac{1}{2}x} \right)\\ = - 6{y^2} + 4xy - 2{x^2}\end{array}\)
Câu 2 :
Giá trị của đa thức \({x^3}y - 14{y^3} - 6x{y^2} + y + 2\) tại x = -1 ; y = 0,5 là:
Đáp án : D Phương pháp giải :
Thay x = -1 ; y = 0,5 vào biểu thức để tính giá trị. Lời giải chi tiết :
Thay x = -1 ; y = 0,5 vào biểu thức, ta được: \(\begin{array}{l}{( - 1)^3}.0,5 - 14{(0,5)^3} - 6( - 1){(0,5)^2} + 0,5 + 2\\ = - 0,5 - 14.0,125 + 6.0,25 + 0,5 + 2\\ = - 0,5 - 1,75 + 1,5 + 0,5 + 2\\ = 1,75\end{array}\)
Câu 3 :
Phân thức \(\frac{2}{{x - 3}}\) không có nghĩa khi:
Đáp án : A Phương pháp giải :
Phân thức không có nghĩa khi mẫu thức bằng 0. Lời giải chi tiết :
Phân thức \(\frac{2}{{x - 3}}\) không có nghĩa khi x – 3 = 0 hay x = 3.
Câu 4 :
Phân thức nghịch đảo của phân thức \(\frac{2}{{x - 4}}\left( {x \ne 4} \right)\) là:
Đáp án : A Phương pháp giải :
Hai phân thức được gọi là nghịch đảo nếu tích của chúng bằng 1. Lời giải chi tiết :
Phân thức nghịch đảo của phân thức \(\frac{2}{{x - 4}}\) là: \(1:\frac{2}{{x - 4}} = \frac{{x - 4}}{2}\).
Câu 5 :
Rút gọn phân thức \(\frac{{x - 3}}{{{x^2} - 9}}\left( {x \ne \pm 3} \right)\), ta được kết quả:
Đáp án : B Phương pháp giải :
Sử dụng các quy tắc tính với phân thức để rút gọn. Lời giải chi tiết :
Ta có: \(\frac{{x - 3}}{{{x^2} - 9}} = \frac{{x - 3}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} = \frac{1}{{x + 3}}\).
Câu 6 :
Hai đường chéo của hình chữ nhật
Đáp án : C Phương pháp giải :
Sử dụng tính chất của hình chữ nhật. Lời giải chi tiết :
Hai đường chéo của hình chữ nhật bằng nhau nên chọn đáp án C.
Câu 7 :
Một tứ giác là hình bình hành nếu nó là:
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về hình bình hành. Lời giải chi tiết :
Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành nên chọn đáp án C.
Câu 8 :
Những tứ giác nào sau đây có hai đường chéo bằng nhau?
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về các hình đã học. Lời giải chi tiết :
Những tứ giác có hai đường chéo bằng nhau là: hình thang cân, hình chữ nhật, hình vuông nên chọn đáp án B.
Câu 9 :
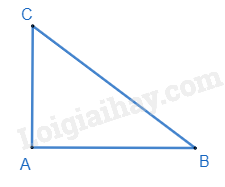
Độ dài một cạnh góc vuông và cạnh huyền của một tam giác vuông lần lượt là 3cm và 5cm. Diện tích của tam giác vuông đó là:
Đáp án : C Phương pháp giải :
Sử dụng định lí Pythagore để tính. Lời giải chi tiết :
Tam giác ABC vuông tại A có AC = 3cm, BC = 5cm. Áp dụng định lí Pythagore vào tam giác ABC, ta có: \(A{B^2} + A{C^2} = B{C^2}\) \(\begin{array}{l} \Rightarrow A{B^2} = B{C^2} - A{C^2} = {5^2} - {3^2} = 16\\ \Rightarrow AB = \sqrt {16} = 4(cm)\end{array}\) Diện tích của tam giác vuông đó là: \({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}4.3 = 6\left( {c{m^2}} \right)\).
Câu 10 :
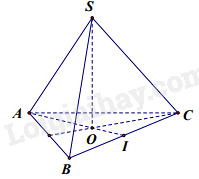
Cho hình khối chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 2a. Tính thể tích V của khối chóp S.ABC.
Đáp án : B Phương pháp giải :
Sử dụng tính chất đường trung bình. Lời giải chi tiết :
Gọi I là trung điểm của cạnh BC, vì tam giác ABC là tam giác đều nên AI là đường trung tuyến đồng thời là đường cao của tam giác ABC. Áp dụng định lí Pythagore vào tam giác ABI, ta có: \(\begin{array}{l}A{I^2} = A{B^2} - B{I^2} = {a^2} - {\left( {\frac{a}{2}} \right)^2} = \frac{{3{a^2}}}{4}\\ \Rightarrow AI = \sqrt {\frac{{3{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}\end{array}\)\(\) \(AO = \frac{2}{3}AI = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\) (O là trọng tâm) Áp dụng định lí Pythagore vào tam giác SOA, ta có: \(\begin{array}{l}S{O^2} = S{A^2} - A{O^2} = {\left( {2a} \right)^2} - {\left( {\frac{{a\sqrt 3 }}{3}} \right)^2} = \frac{{11{a^2}}}{3}\\ \Rightarrow SO = \sqrt {\frac{{11{a^2}}}{3}} = \frac{{a\sqrt {33} }}{3}\end{array}\) Vậy thể tích khối chóp S.ABC là: \(\begin{array}{l}V = \frac{1}{3}.SO.{S_{ABC}} = \frac{1}{3}.\frac{{a\sqrt {33} }}{3}\left( {\frac{1}{2}\frac{{a\sqrt 3 }}{2}.a} \right)\\ = \frac{{{a^3}\sqrt {11} }}{{12}}\end{array}\)
Câu 11 :
Một hình chóp tứ giác đều S.ABCD có độ dài trung đoạn là 12cm và đáy là hình vuông có chu vi là 40cm. Diện tích xung quanh của hình chóp tứ giác đều đó là:
Đáp án : D Phương pháp giải :
Sử dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều. Lời giải chi tiết :
Diện tích xung quanh của hình chóp tứ giác đều đó là: \({S_{xq}} = \frac{{40}}{2}.12 = 240\left( {c{m^2}} \right)\)
Câu 12 :
Nhà bác học Galileo Galilei (1564 – 1642) là người đầu tiên phát hiện ra quan hệ giữa quãng đường chuyển động y (m) và thời gian chuyển động x (giây) của một vật được biểu diễn gần đúng bởi hàm số \(y = 5{x^2}\). Quãng đường mà vật đó chuyển động được sau 3 giây là :
Đáp án : B Phương pháp giải :
Thay x = 3 vào hàm số. Lời giải chi tiết :
Với x = 3 thì \(y = {5.3^2} = 45\)(m). Vậy quãng đường mà vật đó chuyển động được sau 3 giây là 45m.
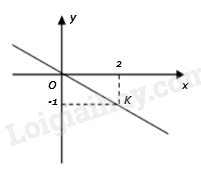
Đáp án : B Phương pháp giải :
Quan sát đồ thị để xác định điểm O; K. Lời giải chi tiết :
Ta có tọa độ điểm O là O(0; 0); tọa độ điểm K là K(2; -1). Gọi hàm số cần tìm là \(y = ax + b\left( {a \ne 0} \right)\). Vì đồ thị của hàm số đi qua điểm O(0; 0) và điểm K nên ta có: \(0 = a.0 + b\)\( \Leftrightarrow \)\(b = 0 \Rightarrow y = ax\) \( - 1 = a.2\)\( \Leftrightarrow \)\(a = \frac{{ - 1}}{2}\)\( \Rightarrow y = - \frac{1}{2}x = y = - 0,5x\). * Học sinh cũng có thể thay tọa độ điểm O và K vào các hàm số trong đáp án để tìm hàm số.
Câu 14 :
Xác định đường thẳng \(y = ax + b;(a \ne 0)\) có hệ số góc bằng 2 và đi qua điểm A (2;1)
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về hệ số góc và hàm số bậc nhất để xác định. Lời giải chi tiết :
Vì đường thẳng có hệ số góc bằng 2 nên a = 2 => y = 2x + b. Vì đường thẳng đi qua điểm A(2; 1) nên 1 = 2.2 + b hay b = -3 => y = 2x - 3.
Câu 15 :
“Trên mặt phẳng, ta vẽ hai trục số Ox, Oy …… với nhau và ……. tại gốc tọa độ O của mỗi trục. Khi đó ta có hệ trục tọa độ Oxy”. Các từ lần lượt cần điền đó là :
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về mặt phẳng tọa độ. Lời giải chi tiết :
“Trên mặt phẳng, ta vẽ hai trục số Ox, Oy vuông góc với nhau và cắt nhau tại gốc tọa độ O của mỗi trục. Khi đó ta có hệ trục tọa độ Oxy”
II. Tự luận
Phương pháp giải :
Sử dụng các phép tính với đa thức để rút gọn biểu thức. Lời giải chi tiết :
a) \(A = 2xy + \frac{1}{2}x.\left( {2x - 4y + 4} \right) - x\left( {x + 2} \right)\) \(\begin{array}{l} = 2xy + {x^2} - 2xy + 2x - {x^2} - 2x\\ = 0\end{array}\) Vì A = 0 nên biểu thức A không phụ thuộc vào giá trị của biến. b) \(B = {\left( {x + 2} \right)^2} - {\left( {x - 3} \right)^2} - 10x\) \(\begin{array}{l} = {\left( {x + 2} \right)^2} - {\left( {x - 3} \right)^2} - 10x\\ = \left( {x + 2 - x + 3} \right)\left( {x + 2 + x - 3} \right) - 10x\\ = 5\left( {2x - 1} \right) - 10x\\ = 10x - 5 - 10x\\ = - 5\end{array}\) Vì B = -5 nên biểu thức B không phụ thuộc vào giá trị của biến. Phương pháp giải :
a) Xác định điều kiện xác định của M. Sử dụng các quy tắc tính của phân thức để rút gọn M. b) Để phân thức M nguyên thì tử thức chia hết cho mẫu thức. Lời giải chi tiết :
a) Ta có: \(M = \frac{{2\left( {1 - 9{x^2}} \right)}}{{3{x^2} + 6x}}:\frac{{2 - 6x}}{{3x}}\left( {x \ne 0;x \ne - 2} \right)\) \(\begin{array}{l} = \frac{{2\left( {1 - 3x} \right)\left( {1 + 3x} \right)}}{{3x\left( {x + 2} \right)}}:\frac{{2(1 - 3x)}}{{3x}}\\ = \frac{{2\left( {1 - 3x} \right)\left( {1 + 3x} \right)}}{{3x\left( {x + 2} \right)}}.\frac{{3x}}{{2\left( {1 - 3x} \right)}}\\ = \frac{{1 + 3x}}{{x + 2}}\end{array}\) Vậy \(M = \frac{{1 + 3x}}{{x + 2}}\). b) Ta có: \(M = \frac{{1 + 3x}}{{x + 2}} = \frac{{3x + 6 - 5}}{{x + 2}} = 3 - \frac{5}{{x + 2}}\) Để M nguyên thì \(\frac{5}{{x + 2}}\) nguyên, hay \(\left( {x + 2} \right) \in U\left( 5 \right) = \left\{ { \pm 1; \pm 5} \right\}\). Ta có bảng giá trị sau:
Vậy \(x \in \left\{ { - 3; - 2; - 7;3} \right\}\) thì M có giá trị nguyên. Phương pháp giải :
a) Thay x = 0 và y = 100; x = 3600 và y = 87 vào hàm số y = ax + b để xác định a và b. b) Thay x = 1500 m để tính nhiệt độ sôi của nước ở thành phố này. Lời giải chi tiết :
a) Thành phố Hồ Chí Minh có độ cao xem như ngang mực nước biển (x = 0m) thì nước có nhiệt độ số là y = \({100^0}C\) nên (0; 100) thuộc đồ thị hàm số y = ax + b => 100 = a.0 + b hay b = 100 => y = ax + 100. Thủ đô La Paz của Bolivia, Nam Mỹ có độ cao x = 3600 m so với mực nước biển thì nhiệt độ sôi của nước là y = \({87^0}C\) nên (3600; 87) thuộc đồ thị hàm số y = ax + 100 => 87 = a.3600 + 100 => a = \( - \frac{{13}}{{3600}}\). Do đó \(y = - \frac{{13}}{{3600}}x + 100\). b) Thành phố Đà Lạt có độ cao 1500 m so với mực nước biển nên x = 1500. Thay x = 1500, ta được: \(y = - \frac{{13}}{{3600}}.1500 + 100 \approx 95\left( {^0C} \right)\). Phương pháp giải :
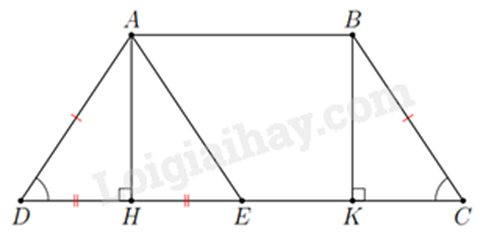
1. Dựa vào định lí Pythagore và công thức tính thể tích giá đèn cầy để tính. 2. a) Tứ giác \(ABKH\) là hình chữ nhật. b) \(\Delta ADH = \Delta BKC\) (ch - gn). Nên suy ra \(DH = KC\). c) Dễ thấy \(HE + EK = EK + KC\) \( \Rightarrow \) \(AB = EC\). Do đó, \(ABCE\) là hình bình hành. Lời giải chi tiết :
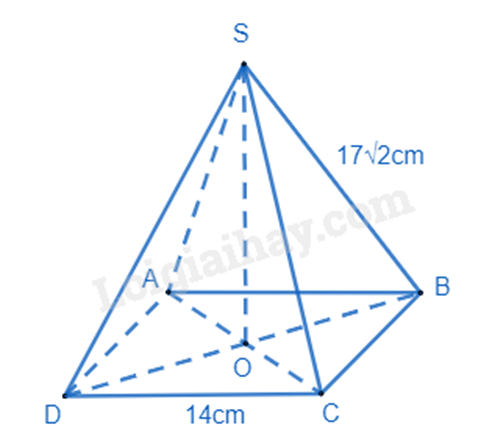
1.
Hình chóp tứ giác đều S.ABCD có đáy là hình vuông, SO là đường cao của hình chóp S.ABCD. Xét tam giác ABC vuông tại B, áp dụng định lí Pythagore, ta có: \(A{C^2} = A{B^2} + B{C^2} = {14^2} + {14^2} = 128\) suy ra \(AC = \sqrt {128} = 14\sqrt 2 (cm)\) Do đó \(AO = \frac{{14\sqrt 2 }}{2} = 7\sqrt 2 (cm)\) Xét tam giác SAO vuông tại O, áp dụng định lí Pythagore, ta có: \(S{O^2} = S{A^2} - A{O^2} = {\left( {17\sqrt 2 } \right)^2} - {\left( {7\sqrt 2 } \right)^2} = 480\) suy ra \(SO = 4\sqrt {30}(cm)\) Thể tích giá đèn cầy S.ABCD là: \(V = \frac{1}{3}{.4\sqrt {30}.14^2} \approx 1431\left( {c{m^3}} \right)\) Vậy thể tích giá đèn cầy là 1431cm3. 2.
a) Ta có: AB // CD (ABCD là hình thang cân), AH \( \bot \) CD => AH \( \bot \) AB => \(\widehat {BAH} = {90^0}\). Xét tứ giác ABKH có: \(\widehat {BAH} = {90^0};\widehat H = {90^0};\widehat K = {90^0}\) suy ra ABKH là hình chữ nhật. b) ABKH là hình chữ nhật => AH = BK. ABCD là hình thang cân nên AD = BC. Xét tam giác AHD và BKC có: \(\left\{ \begin{array}{l}AD = BC\\AH = BK(cmt)\\\widehat H = \widehat K = {90^0}\end{array} \right. \Rightarrow \Delta AHD = \Delta BKC(ch - cgv)\) => DH = CK. (đpcm) c) Ta có: AB = HK (ABKH là hình chữ nhật) Ta có E đối xứng với D qua H => DH = HE => HK = HE + EK = DH + EK = KC + EK = EC. => AB = EC. Mà AB // CE, do đó ABCE là hình bình hành. Phương pháp giải :
Biến đổi biểu thức bằng cách sử dụng hằng đẳng thức. Lời giải chi tiết :
Ta có: \(4{x^2} - 12x + 15 = \left( {4{x^2} - 2.2x.3 + 9} \right) + 6 = {\left( {2x - 3} \right)^2} + 6\). Vì \({\left( {2x - 3} \right)^2} \ge 0,\forall x \in \mathbb{R}\) nên \({\left( {2x - 3} \right)^2} + 6 \ge 6,\forall x \in \mathbb{R}\). Dấu “=” xảy ra là giá trị nhỏ nhất của biểu thức A. \(\min A = 6 \Leftrightarrow 2x - 3 = 0 \Leftrightarrow x = \frac{3}{2}\). Vậy giá trị nhỏ nhất của biểu thức A là 6 khi \(x = \frac{3}{2}\).
|