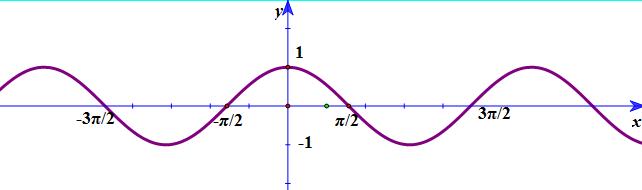
Đề kiểm tra 45 phút (1 tiết) – Chương 1 – Đề số 1 – Đại số và giải tích 11

Đề bài

I. PHẦN TRẮC NGHIỆM

Câu 1: Với những giá trị nào của $x$ thì giá trị của các hàm số tương ứng sau bằng nhau $y = \tan 3x$ và $\tan (\dfrac{\pi }{3} - 2x)$

A. $x = \dfrac{\pi }{{15}} + k\dfrac{\pi }{5},\,k \in \mathbb{Z}$

B.  $x = \dfrac{\pi }{{15}} + k\pi ,\,k \in \mathbb{Z}$

C. $x = \dfrac{\pi }{{15}} + k\dfrac{\pi }{2},\,k \in \mathbb{Z}$

D. $x = \dfrac{\pi }{5} + k\dfrac{\pi }{5},\,k \in \mathbb{Z}$

Câu 2: Tìm m để phương trình $\dfrac{{\cos x + 2\sin x + 3}}{{2\cos x - \sin x + 4}} = m$ có nghiệm.

A. $- 3 \le m \le 2$              B. $m > 2$

C. $m \ge  - 3$                     D. $\dfrac{2}{{11}} \le m \le 2$

Câu 3: Nghiệm của phương trình  $\sin x + \sqrt 3 \cos x = \sqrt 2$ là:

A. $x =  - \dfrac{\pi }{{12}} + k2\pi ,\;x = \dfrac{{5\pi }}{{12}} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).$

B. $x =  - \dfrac{\pi }{4} + k2\pi ,\;x = \dfrac{{3\pi }}{4} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).$

C. $x = \dfrac{\pi }{3} + k2\pi ,\;x = \dfrac{{2\pi }}{3} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).$

D. $x =  - \dfrac{\pi }{4} + k2\pi ,\;x =  - \dfrac{{5\pi }}{4} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).$

Câu 4 : Chọn mệnh đề đúng:

A. Hàm số $y = \sin x$ có chu kỳ $T = \pi$

B. Hàm số $y = \cos x$ và hàm số $y = \tan x$ có cùng chu kỳ.

C. Hàm số $y = \cot x$ và hàm số $y = \tan x$ có cùng chu kỳ.

D. Hàm số $y = \cot x$ có chu kỳ $T = 2\pi$

Câu 5: Nghiệm dương bé nhất của phương trình $2{\sin ^2}x + 5\sin x - 3 = 0$  là:

A. $x = \dfrac{\pi }{3}.$     B. $x = \dfrac{\pi }{{12}}.$

C. $x = \dfrac{\pi }{6}.$     D. $x = \dfrac{{5\pi }}{6}.$

Câu 6: Hàm số nào sau đây có đồ thị không là đường hình sin?

A. $y = \sin x$                        B. $y = \cos x$

C. $y = \sin 2x$                      D. $y = \cot x$

Câu 7: Tập xác định của hàm số$y = f(x) = 2\cot (2x - \dfrac{\pi }{3}) + 1$ là:

A. $\mathbb{R}\backslash \left\{ {\dfrac{\pi }{6} + k2\pi ,k \in \mathbb{Z}} \right\}$   

B. $\mathbb{R}\backslash \left\{ {\dfrac{\pi }{6} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}$

C. $\mathbb{R}\backslash \left\{ {\dfrac{\pi }{6} + k\pi ,k \in \mathbb{Z}} \right\}$     

D. $\mathbb{R}\backslash \left\{ {\dfrac{{5\pi }}{{12}} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}$

Câu 8: Nghiệm của phương trình $\tan (x - \dfrac{\pi }{2}) = \sqrt 3$ là:

A. $x = \dfrac{{5\pi }}{6} + k\pi$.                            

B. $x = \dfrac{{5\pi }}{6} + k2\pi$.                          

C. $x = \dfrac{\pi }{6} + k2\pi$.                               

D. $x = \dfrac{\pi }{6} + k\pi$.

Câu 9: Tập nghiệm của phương trình $\cos 3x =  - 1$ là:

A. $\left\{ { - \dfrac{\pi }{2} + k2\pi |k \in \mathbb{Z}} \right\}.$ 

B. $\left\{ {\pi  + k2\pi |k \in \mathbb{Z}} \right\}.$

C. $\left\{ {\dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}|k \in \mathbb{Z}} \right\}.$       

D. $\left\{ {\dfrac{{k2\pi }}{3}|k \in \mathbb{Z}} \right\}.$

Câu 10: Trong các hàm số sau, hàm số nào là hàm số chẵn.

A. $y = \sin \left| {2016x} \right| + c{\rm{os}}2017x$.    

B. $y = 2016\cos x + 2017\sin x$.

C. $y = \cot 2015x - 2016\sin x$. 

D. $y = \tan 2016x + \cot 2017x$.

Câu 11: Nghiệm của phương trình $\sin 2x = \dfrac{{\sqrt 2 }}{2}$ là:

A.$\,x = \dfrac{\pi }{8} + k2\pi ;x = \dfrac{{3\pi }}{8} + k2\pi (k \in Z)$

B. $\,x = \dfrac{\pi }{4} + k2\pi ;x = \dfrac{{3\pi }}{4} + k2\pi \,(k \in Z)$

C.   $\,x = \dfrac{\pi }{4} + k\pi ;x = \dfrac{{3\pi }}{4} + k\pi (k \in Z)$

D. $\,x = \dfrac{\pi }{8} + k\pi ;x = \dfrac{{3\pi }}{8} + k\pi ;k \in Z)$

Câu 12: Giá trị nhỏ nhất m của hàm số $y = 3\sin x + 1$ là.

A. m = 4                               B. m = -2 

C. m = 3                               D. m = 1

Câu 13: Tập xác định của hàm số $y = f(x) = \dfrac{1}{{\sqrt {1 - sinx} }}$

A. $\mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}$        

B. $\mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}$                 

C. $\mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}$               

D. $\phi$

Câu 14: Giá trị nhỏ nhất của hàm số $y = {\sin ^2}x - 4\sin x - 5$ là:

A. -9                                     B. 0

C. 9                                      D. -8

Câu 15: Đồ thị hàm số nào dưới đây nhận trục tung làm trục đối xứng?

A. $y = \sin x - \cos x$.

B. $y = 2\sin x$.

C. $y = 2\sin \left( { - x} \right)$.

D. $y =  - 2\cos x$

Câu 16: Nghiệm của phương trình $2{\sin ^2}x + \sin x\cos x - 3{\cos ^2}x = 0$ là:

A. $x = \dfrac{\pi }{4} + k\pi$; $x = \arctan ( - \dfrac{3}{2}) + k\pi ,k \in \mathbb{Z}$

B. $x = \dfrac{\pi }{4} + k\pi ,k \in \mathbb{Z}$

C. $x = \dfrac{\pi }{4} + k\pi$;$x = \arctan ( - 3) + k\pi ,k \in \mathbb{Z}$

D. $x = \arctan ( - \dfrac{3}{2}) + k\pi ,k \in \mathbb{Z}$

Câu 17: Phương trình lượng giác nào dưới đây có nghiệm là: $x = \dfrac{\pi }{6} + k\pi ,k \in \mathbb{Z}.$

A. $\cos 2x = \dfrac{{\sqrt 3 }}{2}.$                          

B. $\cot x = \sqrt 3 .$    

C. $\tan x = \sqrt 3 .$     

D. $\sin \left( {x - \dfrac{\pi }{3}} \right) =  - \dfrac{1}{2}$

Câu 18: Giá trị lớn nhất M của hàm số $y = \sin x + \cos x$ là.

A. $M = 2$                         

B. $M = 2\sqrt 2$             

C. $M = 1$                         

D. $M = \sqrt 2$

Câu 19: Nghiệm của phương trình $\sin x = \cos x$ là:

A. $x = \dfrac{\pi }{4} + k2\pi$.                               

B. $x = \dfrac{\pi }{4} + k\pi$.                                 

C. $x = \dfrac{\pi }{4}$.    

D. $x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}$.

Câu 20: Đồ thì hình bên là đồ thị của hàm số nào?

A. $y = \sin x$                     B. $y = \cot x$    

C. $y = \tan x$                    D. $y = \cos x$           

II. PHẦN TỰ LUẬN

Câu 21: Giải các phương trình sau

a) $\sin 3x - \cos 2x = 0$                                             

b) $\dfrac{{\sin x + \sqrt 3 \cos x}}{{\sin x - \cos \dfrac{\pi }{4}}} = 0$

Câu 22: Giải phương trình :   $2{\cos ^2}\left( {\dfrac{\pi }{4} - 2x} \right) + \sqrt 3 \cos 4x = 4{\cos ^2}x - 1$

Lời giải chi tiết

I. PHẦN TRẮC NGHIỆM

Câu 1:

Ta có: $\tan 3x = \tan (\dfrac{\pi }{3} - 2x)$$\Leftrightarrow 3x = \dfrac{\pi }{3} - 2x + k\pi \;\left( {k \in \mathbb{Z}} \right)$

$\Leftrightarrow 5x = \dfrac{\pi }{3} + k\pi \left( {k \in \mathbb{Z}} \right)$

$\Leftrightarrow x = \dfrac{\pi }{{15}} + k\dfrac{\pi }{5}\;\left( {k \in \mathbb{Z}} \right)$

Chọn đáp án A.

Câu 2:

Ta có: $\dfrac{{\cos x + 2\sin x + 3}}{{2\cos x - \sin x + 4}} = m$

$\Leftrightarrow \cos x + 2\sin x + 3 = m\left( {2\cos x - \sin x + 4} \right)$

$\Leftrightarrow \left( {2m - 1} \right)\cos x - \left( {m + 2} \right)\sin x = 3 - 4m$

Điều kiện có nghiệm: ${\left( {2m - 1} \right)^2} + {\left( {m + 2} \right)^2} \ge {\left( {3 - 4m} \right)^2}$

$\Leftrightarrow 4{m^2} - 4m + 1 + {m^2} + 4m + 4$$\ge 9 - 24m + 16{m^2}$

$\Leftrightarrow 11{m^2} - 24m + 4 \le 0$$\Leftrightarrow \dfrac{2}{{11}} \le m \le 2.$

Chọn đáp án D.

Câu 3:

Ta có:$\sin x + \sqrt 3 \cos x = \sqrt 2$

$\begin{array}{l} \Leftrightarrow \frac{1}{2}\sin x + \frac{{\sqrt 3 }}{2}\cos x = \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow \cos \frac{\pi }{3}\sin x + \sin \frac{\pi }{3}\cos x = \frac{{\sqrt 2 }}{2} \end{array}$

$\Leftrightarrow \sin \left( {x + \dfrac{\pi }{3}} \right) = \dfrac{{\sqrt 2 }}{2}$

$\Leftrightarrow \sin \left( {x + \dfrac{\pi }{3}} \right) = \sin \dfrac{\pi }{4}$$\Leftrightarrow \left[ \begin{array}{l}x + \dfrac{\pi }{3} = \dfrac{\pi }{4} + k2\pi \\x + \dfrac{\pi }{3} = \pi  - \dfrac{\pi }{4} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)$

$\Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{\pi }{{12}} + k2\pi \\x = \dfrac{{5\pi }}{{12}} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)$

Chọn đáp án A.

Câu 4:

+ Hàm số $y = \sin x,\,y = \cos x$ có chu kỳ là $T = 2\pi$

+ Hàm số $y = \tan x,y = \cot x$ có chu kì là $T = \pi$

Chọn đáp án C.

Câu 5:

Ta có: $2{\sin ^2}x + 5\sin x - 3 = 0$$\Leftrightarrow \left( {2\sin x - 1} \right)\left( {\sin x + 3} \right) = 0$

$\Leftrightarrow \sin x = \dfrac{1}{2}$$\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)$

Nghiệm dương bé nhất của phương trình là $x = \dfrac{\pi }{6}.$

Chọn đáp án C.

Câu 6:

Hàm số $y = \cot x$ có đồ thị không là đường hình sin.

Chọn đáp án D.

Câu 7:

$y = f(x) = 2\cot (2x - \dfrac{\pi }{3}) + 1$$= \dfrac{{2\cos (2x - \dfrac{\pi }{3})}}{{\sin (2x - \dfrac{\pi }{3})}} + 1$

ĐKXĐ: $\sin \left( {2x - \dfrac{\pi }{3}} \right) \ne 0$

$\Leftrightarrow \left( {2x - \dfrac{\pi }{3}} \right) \ne k\pi \;\left( {k \in \mathbb{Z}} \right)$

$\Leftrightarrow x \ne \dfrac{\pi }{6} + k\dfrac{\pi }{2}\;\left( {k \in \mathbb{Z}} \right)$
Chọn đáp án B.

Câu 8:

Ta có: $\tan (x - \dfrac{\pi }{2}) = \sqrt 3$

$\Leftrightarrow \tan (x - \dfrac{\pi }{2}) = \tan \dfrac{\pi }{3}$

$\Leftrightarrow x - \dfrac{\pi }{2} = \dfrac{\pi }{3} + k\pi \;\left( {k \in \mathbb{Z}} \right)$

$\Leftrightarrow x = \dfrac{{5\pi }}{6} + k\pi \;\left( {k \in \mathbb{Z}} \right)$

Chọn đáp án A.

Câu 9:

Ta có: $\cos 3x =  - 1 \Leftrightarrow 3x = \pi  + k2\pi \,\left( {k \in \mathbb{Z}} \right)$

$\Leftrightarrow x = \dfrac{\pi }{3} + k\dfrac{{2\pi }}{3}\;\left( {k \in \mathbb{Z}} \right)$

Chọn đáp án C.

Câu 10:

Đáp án A: TXĐ: D=R.

Ta có: 

$\begin{array}{l} y\left( { - x} \right) = \sin \left| { - 2016x} \right| + \cos \left( { - 2017x} \right)\\ = \sin 2016x + \cos 2017x = y\left( x \right) \end{array}$

Hàm số $y = \sin \left| {2016x} \right| + c{\rm{os}}2017x$ là hàm số chẵn.

Chọn đáp án A.

Câu 11:

Ta có: $\sin 2x = \dfrac{{\sqrt 2 }}{2} \Leftrightarrow \sin 2x = \sin \dfrac{\pi }{4}$

$\Leftrightarrow \left[ \begin{array}{l}2x = \dfrac{\pi }{4} + k2\pi \\2x = \pi  - \dfrac{\pi }{4} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)$

$\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{8} + k\pi \\x = \dfrac{{3\pi }}{8} + k\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)$

Chọn đáp án D.

Câu 12:

Ta có: $\sin x \in \left[ { - 1;1} \right]$

$\begin{array}{l} \Rightarrow - 1 \le \sin x \le 1\\ \Rightarrow - 3 \le 3\sin x \le 3\\ \Rightarrow - 2 \le 3\sin x + 1 \le 4 \end{array}$

Chọn đáp án B.

Câu 13:

Ta có: $\sin x \in \left[ { - 1;1} \right] \Rightarrow 1 - \sin x \in \left[ {0;2} \right]$

Điều kiện xác định: $1 - \sin x \ne 0 \Leftrightarrow \sin x \ne 1$

$\Leftrightarrow x \ne \dfrac{\pi }{2} + k2\pi  \;\left( {k \in \mathbb{Z}} \right)$

Chọn đáp án C.

Câu 14:

Ta có: $y = {\sin ^2}x - 4\sin x - 5$$= \left( {{{\sin }^2}x - 4\sin x + 4} \right) - 9$$= {\left( {\sin x - 2} \right)^2} - 9$

+ $\sin x \in \left[ { - 1;1} \right] \Rightarrow \sin x - 2 \in \left[ { - 3; - 1} \right]$

$\Leftrightarrow {\left( {\sin x - 2} \right)^2} \in \left[ {1;9} \right]$

Khi đó $y \ge 1 - 9 =  - 8$

Chọn đáp án D.

Câu 15:

Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng, do đó ta kiểm tra hàm số chẵn ở mỗi đáp án.

Dễ thấy hàm số $y =  - 2\cos x$ là hàm chẵn nên nhận trục tung làm trục đối xứng.

Chọn đáp án D.

Câu 16:

Ta có: $2{\sin ^2}x + \sin x\cos x - 3{\cos ^2}x = 0$

$\Leftrightarrow \left( {\sin x - \cos x} \right)\left( {2\sin x + 3\cos x} \right) = 0$

$\Leftrightarrow \left[ \begin{array}{l}\sin x = \cos x\\2\sin x =  - 3\cos x\end{array} \right. \\ \Leftrightarrow \left[ \begin{array}{l}\tan x = 1\\\tan x =  - \dfrac{3}{2}\end{array} \right. \\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{4} + k\pi \\x = \arctan \left( { - \dfrac{3}{2}} \right) + k\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)$

Chọn đáp án A.

Câu 17:

Ta có: $\cot x = \sqrt 3  \Leftrightarrow x = \dfrac{\pi }{6} + k\pi \;\left( {k \in \mathbb{Z}} \right)$

Chọn đáp án B.

Câu 18:

Ta có: $y = \sin x + \cos x = \sqrt 2 \sin \left( {x + \dfrac{\pi }{4}} \right)$

$\begin{array}{l} - 1 \le \sin \left( {x + \frac{\pi }{4}} \right) \le 1\\ \Rightarrow - \sqrt 2 \le \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right) \le \sqrt 2 \end{array}$

$\Rightarrow y \in \left[ { - \sqrt 2 ;\sqrt 2 } \right]$

Chọn đáp án D.

Câu 19:

Ta có: $\sin x = \cos x \Leftrightarrow \tan x = 1$

$\Leftrightarrow x = \dfrac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)$

Chọn đáp án B.

Câu 20:

Đồ thị hình bên là của hàm số $y = \cos x$

Chọn đáp án D.

II. PHẦN TỰ LUẬN

Câu 21:

$a)  \sin 3x - \cos 2x = 0 \Leftrightarrow \sin 3x = \cos 2x$$\Leftrightarrow \sin 3x = \sin \left( {\dfrac{\pi }{2} - 2x} \right)$

$\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l} 3x = \frac{\pi }{2} - 2x + k2\pi \\ 3x = \pi - \frac{\pi }{2} + 2x + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} 5x = \frac{\pi }{2} + k2\pi \\ x = \frac{\pi }{2} + k2\pi \end{array} \right. \end{array}$

$\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \dfrac{\pi }{{10}} + k\dfrac{{2\pi }}{5}}\\{x = \dfrac{\pi }{2} + k2\pi }\end{array}} \right.$

Vậy phương trình có nghiệm: $x = \dfrac{\pi }{{10}} + k\dfrac{{2\pi }}{5};\,\,x = \dfrac{\pi }{2} + k2\pi$

$b) \dfrac{{\sin x + \sqrt 3 \cos x}}{{\sin x - \cos \dfrac{\pi }{4}}} = 0 \, (1)$

ĐK: $\sin x - \cos \dfrac{\pi }{4} \ne 0$

$\begin{array}{l} \Leftrightarrow \sin x - \frac{{\sqrt 2 }}{2} \ne 0 \Leftrightarrow \sin x \ne \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow \left\{ \begin{array}{l} x \ne \frac{\pi }{4} + k2\pi \\ x \ne \frac{{3\pi }}{4} + k2\pi \end{array} \right.\,\,\,\,\,\,\,\left( * \right) \end{array}$

$\begin{array}{l}(1) \Leftrightarrow \sin x + \sqrt 3 \cos x = 0 \\\Leftrightarrow \dfrac{1}{2}\sin x + \dfrac{{\sqrt 3 }}{2}\cos x = 0 \\\Leftrightarrow \cos \dfrac{\pi }{3}\sin x + \sin \dfrac{\pi }{3}\cos x = 0\\ \Leftrightarrow \sin (x + \dfrac{\pi }{3}) = 0 \Leftrightarrow x + \frac{\pi }{3} = k\pi \\ \Leftrightarrow x = \dfrac{{ - \pi }}{3} + k\pi \end{array}$

Kết hợp với điều kiện (*) ta thấy thỏa mãn.

Vậy phương trình có nghiệm: $x = \dfrac{{ - \pi }}{3} + k\pi$

Câu 22:

$2{\cos ^2}\left( {\dfrac{\pi }{4} - 2x} \right) + \sqrt 3 \cos 4x = 4{\cos ^2}x - 1$

$\Leftrightarrow 1 + \cos \left( {\dfrac{\pi }{2} - 4x} \right) + \sqrt 3 \cos 4x = 4{\cos ^2}x - 1$$\Leftrightarrow \sin 4x + \sqrt 3 \cos 4x = 2\left( {2{{\cos }^2}x - 1} \right)$

$\begin{array}{l} \Leftrightarrow \dfrac{1}{2}\sin 4x + \dfrac{{\sqrt 3 }}{2}\cos 4x = \cos 2x \\\Leftrightarrow \sin \dfrac{\pi }{6}\sin 4x + \cos \dfrac{\pi }{6}\cos 4x = \cos 2x\\ \Leftrightarrow \cos \left( {4x - \dfrac{\pi }{6}} \right) = \cos 2x \end{array}$

$\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l} 4x - \frac{\pi }{6} = 2x + k2\pi \\ 4x - \frac{\pi }{6} = - 2x + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} 2x = \frac{\pi }{6} + k2\pi \\ 6x = \frac{\pi }{6} + k2\pi \end{array} \right. \end{array}$

$\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \dfrac{\pi }{{12}} + k\pi }\\{x = \dfrac{\pi }{{36}} + k\dfrac{\pi }{3}}\end{array}} \right.\,\,(k \in \mathbb{Z})$

Vậy phương trình có nghiệm là: $x = \dfrac{\pi }{{12}} + k\pi ;\,x = \dfrac{\pi }{{36}} + k\dfrac{\pi }{3}$

HocTot.Nam.Name.Vn