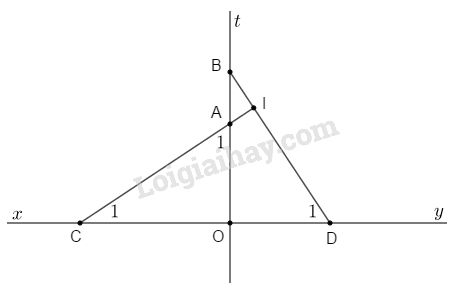
Đề kiểm tra 15 phút - Đề số 6 - Bài 2,3,4,5 - Chương 2 - Hình học 7

Đề bài

Cho góc bẹt \(\widehat {xOy}\) có phân giác Ot. Trên Ot lấy hai điểm A và B (A nằm giữa O và B). Lấy điểm C thuộc Ox, sao cho OC = OB. Lấy điểm D thuộc Oy sao cho OD = OA. Chứng minh:

a) \(AC= BD\)     

b) \(AC \bot BD.\)

Lời giải chi tiết

a) Ot là tia phân giác của góc bẹt \(\widehat {xOy}\) nên

\(\widehat {CID} = {180^o} - \left( {\widehat {{C_1}} + \widehat {{D_1}}} \right) \)\(\,= {180^o} - {90^o} = {90^o}\)

\(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}} }{ 2} = \dfrac{{{{180}^o}}}{ 2} = {90^o}.\)

Xét \(\Delta AOC\) và \(\Delta DOB\) có:

+) \(OA = OD\) (giả thiết)

+) \(\widehat {COA} = \widehat {BOD} = {90^o}\) (chứng minh trên)

+) \(OC = OB\) (giả thiết)

Vậy \(\Delta AOC=\Delta DOB\) (c.g.c)

\( \Rightarrow AC = BD.\)

b) \(\Delta AOC=\Delta DOB\) (chứng minh trên)

\( \Rightarrow \widehat {{A_1}} = \widehat {{D_1}}\) (góc tương ứng)

mà \(\widehat {{A_1}} + \widehat {{C_1}} = {90^o}\) (vì \(\widehat {AOC} = {90^o}\)\( \Rightarrow \widehat {{C_1}} + \widehat {{D_1}} = {90^o}.\)

Gọi I là giao điểm của AC và BD.

Xét \(\Delta AID\) ta có:

\(\widehat {CID} = {180^o} - \left( {\widehat {{C_1}} + \widehat {{D_1}}} \right)\)\(\, = {180^o} - {90^o} = {90^o}\)

Chứng tỏ \(AC \bot BD.\)

HocTot.Nam.Name.Vn