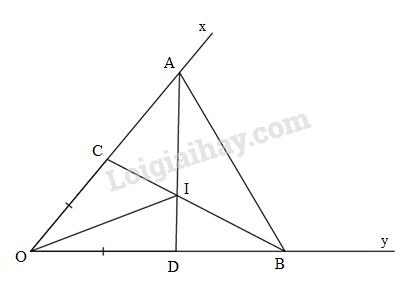
Đề kiểm tra 15 phút - Đề số 5 - Bài 2,3,4,5 - Chương 2 - Hình học 7

Đề bài

Cho góc  \(\widehat {xOy}\). Lấy A, C thuộc tia Ox sao cho OC< OA. Trên tia Oy lấy B và D sao cho \(OB = OA,\,OD = OC.\)

a) Chứng minh AD = BC và \(\Delta ABC=\Delta BAD\) 

b) Gọi I là giao điểm của AD và BC. Cho biết IA = IB. Chứng minh OI là tia phân giác của góc \(\widehat {xOy}\).

Lời giải chi tiết

a) Xét \(\Delta ADO\) và \(\Delta BCO\) có:

+) OA = OB (giả thiết)

+) \(\widehat O\) chung

+) OD = OC (giả thiết)

Do đó \(\Delta ADO=\Delta BCO\) (c.g.c)

\( \Rightarrow AD = BC\) (cạnh tương ứng)

Và \(\widehat {ADO} = \widehat {BCO}\) (góc tương ứng).

Mà \(\widehat {ADO} + \widehat {ADB} = {180^o}\) (cặp góc kề bù) và \(\widehat {BCO} + \widehat {BCA} = {180^o}\)

\(\Rightarrow \widehat {ADB} = \widehat {BCA}.\)

Lại có \(OA = OB;\,OC = OD \)

\(\Rightarrow OA - OC = OB - OD\) hay \(AC = BD.\)

Xét \(\Delta ABC\) và \(\Delta BAD\) có:

+) AC = BD (chứng minh trên);

+) \(\widehat {ACB} = \widehat {BDA}\)(chứng minh trên);

+) AD = BC (chứng minh trên).

Do đó: \(\Delta ABC=\Delta BAD\) (c.g.c)

b) Xét \(\Delta OIA\) và \(\Delta OIB\) có:

+) OI chung,

+) IA = IB (giả thiết),

+) OA = OB (giả thiết)

Do đó \(\Delta OIA=\Delta OIB\) (c.c.c)

\( \Rightarrow \widehat {IOA} = \widehat {IOB}\).

Chứng tỏ OI là phân giác của \(\widehat {xOy}\)

HocTot.Nam.Name.Vn