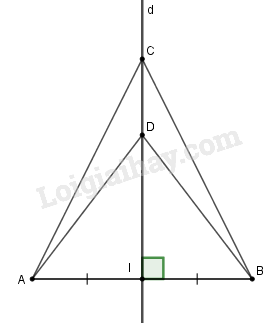
Đề kiểm tra 15 phút - Đề số 2 - Bài 2,3,4,5 - Chương 2 - Hình học 7Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 2,3,4,5 - Chương 2 - Hình học 7 Đề bài Cho đoạn thẳng AB, đường trung trực d của AB tại I, trên cùng một nửa mặt phẳng bờ là đường thẳng AB lấy hai điểm C và D thuộc d (D nằm giữa hai điểm C và I). Hãy so sánh hai góc ADI và góc BDI. Phương pháp giải - Xem chi tiết Mỗi góc ngoài của một tam giác bằng tổng hai góc tổng của hai góc không kề với nó. Lời giải chi tiết
Hai điểm C và D thuộc đường trung trực d của đoạn thẳng AB nên \(\widehat {BDI} = \widehat {BCD} + \widehat {CBD}\) \(\Rightarrow \widehat {ADI} = \widehat {BDI};\) \(CA = CB\) và \(DA = DB\) (tính chất điểm thuộc đường trung trực) Xét \(\Delta ACD\) và \(\Delta BCD\) , có +) CD là cạnh chung, +) \(CA = CB,\,DA = DB\) Do đó \(\Delta ACD=\Delta BCD\) (c.c.c) \( \Rightarrow \widehat {ADC} = \widehat {BDC}\) (hai góc tương ứng). \(\widehat {CAD} = \widehat {CBD}\) (hai góc tương ứng). Mà \(\widehat {ADI}\) và \(\widehat {BDI}\) lần lượt là hai góc ngoài của hai tam giác ADC và BDC, ta có \(\widehat {ADI} = \widehat {ACD} + \widehat {CAD}\) Và \(\widehat {BDI} = \widehat {BCD} + \widehat {CBD}\) \(\Rightarrow \widehat {ADI} = \widehat {BDI}.\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
