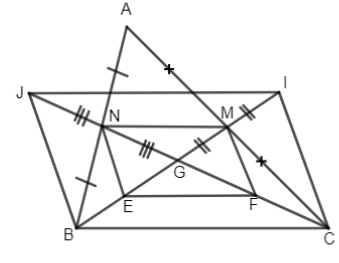
Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 1 - Hình học 8

Đề bài

Cho tam giác ABC, hai trung tuyến BM, CN cắt nhau tại G. Gọi E, F lần lượt là trung điểm của GB và GC.

a) Chứng minh tứ giác MNEF là hình bình hành. 

b) Lấy I, J thuộc tia đối của MG và NG sao cho MI = MG và NI = NG. Chứng minh tứ giác BCIJ là hình bình hành.

Lời giải chi tiết

 

a) Ta có MN là đường trung bình của $\Delta ABC$

$\Rightarrow MN//BC$ và $MN = \dfrac{1}{ 2}BC.$

Lại có EF là đường trung bình của $\Delta BGC$ nên ${\rm{EF}}// BC$ và ${\rm{EF}} = \dfrac{1}{ 2}BC.$

Do đó $MN// {\rm{EF}}$ và $MN = EF.$

Vậy MNEF là hình bình hanh (hai cạnh đối vừa song song vừa bằng nhau).

b) Tam giác ABC có hai trung tuyến BM, CN cắt nhau tại G

Nên G là trọng tâm của $\Delta ABC$, do đó $GN = \dfrac{1 }{ 2}GC$

Mà GN = JN (gt) $\Rightarrow GJ = GC.$

Tương tự ta có $GM = \dfrac{1 }{ 2}GB$ (do G là trọng tâm tam giác ABC) mà $GM=MI$ (gt)

Suy ra GI = GB.

Vậy tứ giác BJIC là hình bình hành (hai đường chéo CJ và BI cắt nhau tại trung điểm mỗi đường).

HocTot.Nam.Name.Vn