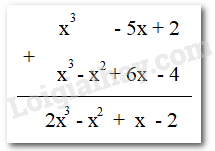Cộng, trừ hai đa thức một biếnCộng, trừ hai đa thức một biến Cách 1: Để cộng (hay trừ) hai đa thức, ta làm như sau: Bước 1: Viết hai đa thức trong dấu ngoặc Bước 2: Thực hiện bỏ dấu ngoặc (theo quy tắc dấu ngoặc) Bước 3: Nhóm các hạng tử đồng dạng Bước 4: Cộng, trừ các đơn thức đồng dạng. Ví dụ: Cho đa thức \(P(x) = 3 + 5{x^2} - 3{x^3} + 4{x^2} - 2x - {x^3} + 5{x^5}.\) Thu gọn và sắp xếp đa thức \(P\left( x \right)\) Giải \(P(x) = 3 + 5{x^2} - 3{x^3} + 4{x^2} - 2x - {x^3} + 5{x^5}\) \( = 5{x^5} + \left( { - 3{x^3} - {x^3}} \right) + \left( {5{x^2} + 4{x^2}} \right) - 2x + 3\) \( = 5{x^5} - 4{x^3} + 9{x^2} - 2x + 3\) Cách 2: Đặt tính cộng sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng theo từng cột: Chú ý: Nếu Q + R = P thì R = P – Q Nếu R = P – Q thì Q + R = P  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
