Bài 9 trang 100 SGK Hình học 12

LG a

Chứng minh rằng các đường thẳng \(AB, AC, AD\) vuông góc với nhau từng đôi một. Tính thể tích khối tứ diện \(ABCD\).

Phương pháp giải:

Ta xét các tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} \); \(\overrightarrow {AB} .\overrightarrow {AD} \); \(\overrightarrow {AC} .\overrightarrow {AD} \)

\( \Rightarrow {V_{ABCD}} = \dfrac{1}{6}AB.AC.AD\)

Lời giải chi tiết:

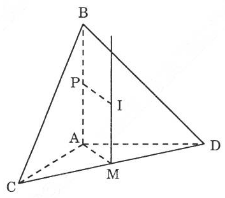
a) Ta xét các tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} \); \(\overrightarrow {AB} .\overrightarrow {AD} \); \(\overrightarrow {AC} .\overrightarrow {AD} \)

Ta có: \(\overrightarrow {AB} = (-1; 0; 0)\), \(\overrightarrow {AC} = (0; 0; 4)\), \(\overrightarrow {AD} = (0; -2; 0)\)

\(\overrightarrow {AB} .\overrightarrow {AC} = (-1).0 + 0.0 + 0.4 = 0\Leftrightarrow \overrightarrow {AB}  \bot \overrightarrow {AC} \)

Các trường hợp còn lại chứng minh tương tự.

Ta có: \(V_{ABCD}\) =\({1 \over 6}.AB.AC.AD\)

Mà \(AB = 1; AC = 4; AD = 2\)

\( \Rightarrow {V_{ABCD}} = {1 \over 6}.1.4.2 = {4 \over 3}\)(đvtt)

LG b

Viết phương trình mặt cầu \((S)\) đi qua bốn điểm \(A, B, C, D\).

Phương pháp giải:

Sử dụng phương pháp xác định tâm mặt cầu ngoại tiếp tứ diện ABCD, xác định tâm I và tính bán kính \(R=IA\).

Lời giải chi tiết:

Gọi \(I(a; b; c)\) là tâm mặt cầu ngoại tiếp tứ diện \(ABCD\).

\(IA = IB = IC\) \( \Rightarrow I\) nằm trên trục của đường tròn ngoại tiếp tam giác \(ACD\). Tam giác \(ACD\) vuông tại đỉnh \(A\) nên trục của đường tròn ngoại tiếp tam giác \(ACD\) là đường thẳng vuông góc với mp \((ACD)\) và đi qua trung điểm \(M\) của cạnh huyền \(CD\).

Như vậy \(MI // AB\)                       (1)

Ta lại có \(IA = IB\). Gọi \(P\) là trung điểm của \(AB\), ta có:

\(MI = AP\) = \({1 \over 2}AB\)                        (2)

Từ (1) và (2), suy ra \(\overrightarrow {MI}  = {1 \over 2}\overrightarrow {AB} \)

Với \(C (2; 4; 3), D (2; 2; -1)\) \( \Rightarrow M (2; 3; 1)\)

\(\overrightarrow {MI}= (a - 2; b - 3; c - 1); \overrightarrow {AB}  = (-1; 0; 0) \)

\(\left\{ \matrix{
a - 2 = {1 \over 2}( - 1) \Rightarrow a = {3 \over 2} \hfill \cr 
b - 3 = {1 \over 2}.0 \Rightarrow b = 3 \hfill \cr 
c - 1 = {1 \over 2}.0 \Rightarrow c = 1 \hfill \cr} \right.\)

Tâm \(I\) của mặt cầu ngoại tiếp tứ diện \(ABCD\) là \(I\)\(\left( {{3 \over 2};3;1} \right)\)

Bán kính của mặt cầu ngoại tiếp tứ diện \(ABCD\) là \(r\) thì:

\(r^2 = IA^2\) =\({\left( {2 - {3 \over 2}} \right)^2} + {(4 - 3)^2} + {( - 1 - 1)^2} = {{21} \over 4}\)

Phương trình mặt cầu ngoại tiếp tứ diện \(ABCD\):

\({\left( {x - {3 \over 2}} \right)^2} + {(y - 3)^2} + {(z - 1)^2} = {{21} \over 4}\).

Cách khác:

Gọi mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} + 2ax + 2by + 2cz + d = 0\) đi qua 4 điểm A, B, C, D.

Khi đó \(\left\{ \begin{array}{l}4 + 16 + 1 + 4a + 8b - 2c + d = 0\\1 + 16 + 1 + 2a + 8b - 2c + d = 0\\4 + 16 + 9 + 4a + 8b + 6c + d = 0\\4 + 4 + 1 + 4a + 4b - 2c + d = 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}4a + 8b - 2c + d =  - 21\\2a + 8b - 2c + d =  - 18\\4a + 8b + 6c + d =  - 29\\4a + 4b - 2c + d =  - 9\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}2a =  - 3\\8b - 2c + d =  - 15\\8b + 6c + d =  - 23\\4b - 2c + d =  - 3\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}a =  - \dfrac{3}{2}\\b =  - 3\\c =  - 1\\d = 7\end{array} \right.\)

Vậy phương trình mặt cầu là: \({x^2} + {y^2} + {z^2} - 3x - 6y - 2z + 7 = 0\) hay \({\left( {x - \dfrac{3}{2}} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 1} \right)^2} = \dfrac{{21}}{4}\)

LG b

Viết phương trình mặt phẳng \((α)\) tiếp xúc với mặt cầu \((S)\) và song song với mặt phẳng \((ABD)\).

Phương pháp giải:

Xác định VTPT của mặt phẳng \(\alpha\), viết phương trình mặt phẳng \(\alpha\) khi biết VTPT.

\(\alpha\) tiếp xúc với (S) \( \Leftrightarrow d\left( {I;\left( \alpha  \right)} \right) = R\) với \(I;R\) lần lượt là tâm và bán kính mặt cầu (S).

Lời giải chi tiết:

Ta có:\(\displaystyle AC ⊥ (ABD)\); \(\displaystyle (α)\)//\(\displaystyle (ABD)\) nên nhận \(\displaystyle \overrightarrow {AC} \) làm vectơ pháp tuyến.

Ta có \(\displaystyle \overrightarrow {AC}  = (0; 0; 4)\) nên \(\displaystyle (α)\):\(\displaystyle z + D = 0\).

Khoảng cách từ tâm \(\displaystyle I\) của mặt cầu đến mặt phẳng \(\displaystyle (α)\) là:

\(\displaystyle d(I,(α)) ={{\left| {1 + D} \right|} \over 1} = \left| {1 + D} \right|\)

Để mặt phẳng \(\displaystyle (α)\) tiếp xúc với mặt cầu, ta cần có:

\(\displaystyle d(I,(α)) = r \Rightarrow \left| {1 + D} \right| = {{\sqrt {21} } \over 2}\)

Ta có hai mặt phẳng:

TH1: \(\displaystyle 1 + D ={{\sqrt {21} } \over 2} \Rightarrow D = {{\sqrt {21} } \over 2} - 1\)

\(\displaystyle \Rightarrow \left( {{\alpha _1}} \right):z + {{\sqrt {21} } \over 2} - 1 = 0\)

TH2: \(\displaystyle 1 + D = - {{\sqrt {21} } \over 2} \Rightarrow D =  - {{\sqrt {21} } \over 2} - 1 \)

\(\displaystyle \Rightarrow \left( {{\alpha _2}} \right):z - {{\sqrt {21} } \over 2} - 1 = 0\)

HocTot.Nam.Name.Vn