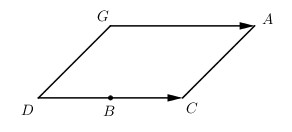
Bài 14 trang 101 SGK Hình học 12

LG a

Xác định điểm $G$ sao cho $\overrightarrow {GA}  + 2\overrightarrow {GB}  - 2\overrightarrow {GC}  = 0.$

Phương pháp giải:

Biến đổi đẳng thức vector trong câu a) theo những điểm cố định và suy ra vị trí của điểm G.

Lời giải chi tiết:

Ta có

$\begin{array}{l} \,\,\,\,\,\,\,\overrightarrow {GA} + 2\overrightarrow {GB} - 2\overrightarrow {GC} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {GA} + 2\left( {\overrightarrow {GB} - \overrightarrow {GC} } \right) = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {GA} + 2\overrightarrow {CB} = 0\\ \Leftrightarrow \overrightarrow {GA} = 2\overrightarrow {BC}  \end{array}$

Gọi $D$ là điểm mà $\overrightarrow {DC}  = 2\overrightarrow {BC}$ tức là điểm $B$ là trung điểm của $CD$ $\Rightarrow \overrightarrow {GA}  = \overrightarrow {DC}$

Vậy $G$ là đỉnh thứ tư của hình bình hành $ACDG$.

LG b

Tìm tập hợp các điểm $M$ sao cho $MA^2 + 2MB^2 - 2MC^2 = k^2$, với $k$ là hằng số.

Phương pháp giải:

Sử dụng công thức ba điểm, chèn điểm G vào tất cả các vector $\overrightarrow {MA} ;\overrightarrow {MB} ;\overrightarrow {MC}$, biến đổi và kết luận.

Lời giải chi tiết:

Gọi $G$ là điểm trong câu a): $\overrightarrow {GA}  + 2\overrightarrow {GB}  - 2\overrightarrow {GC}  = \overrightarrow 0$.

Ta có: $M{A^2} = {\overrightarrow {MA} ^2}= {(\overrightarrow {MG}  + \overrightarrow {GA} )^2}$

$= M{G^2} + G{A^2} + 2\overrightarrow {MG} .\overrightarrow {GA}$;

$M{B^2} = {\overrightarrow {MB} ^2} = {(\overrightarrow {MG}  + \overrightarrow {GB} )^2}$

$= M{G^2} + G{B^2} + 2\overrightarrow {MG} .\overrightarrow {GB}$;

$M{C^2} = {\overrightarrow {MC} ^2} = {(\overrightarrow {MG}  + \overrightarrow {GC} )^2}$

$= M{G^2} + G{C^2} + 2\overrightarrow {MG} .\overrightarrow {GC}$.

Từ đó $MA^2 +2 MB^2 -2 MC^2 = k^2$

$\Leftrightarrow M{G^2} + G{A^2} + 2G{B^2} - 2G{C^2}$

$+ 2\overrightarrow {MG} (\overrightarrow {GA}  + 2\overrightarrow {GB}  - 2\overrightarrow {GC} ) = {k^2}$

$\Leftrightarrow M{G^2} = {k^2} - (G{A^2} + 2G{B^2} - 2G{C^2})$ 

(Vì $\overrightarrow {GA}  + 2\overrightarrow {GB}  - 2\overrightarrow {GC}  = \overrightarrow 0$).

Do vậy:

Nếu $k^2 - (GA^2 + 2GB^2 - 2GC^2) = r^2 > 0$ thì tập hợp các điểm M là mặt cầu tâm G bán kính r.

Nếu $k^2 - (GA^2 + 2GB^2 - 2GC^2) = r^2 =0$ thì tập hợp M chính là điểm G.

Nếu $k^2 - (GA^2 + 2GB^2 - 2GC^2) = r^2 < 0$ thì tập hợp các điểm M chính là tập rỗng.

HocTot.Nam.Name.Vn