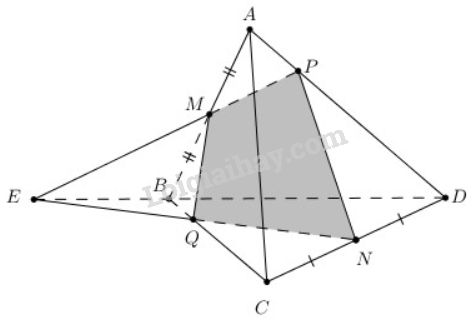
Bài 8 trang 54 SGK Hình học 11

Đề bài

Cho tứ diện $ABCD$. Gọi $M$ và $N$ lần lượt là trung điểm của các cạnh $AB$ và $CD$ trên cạnh $AD$ lấy điểm $P$ không trùng với trung điểm của $AD$

a) Gọi $E$ là giao điểm của đường thẳng $MP$ và đường thẳng $BD$. Tìm giao tuyến của hai mặt phẳng $(PMN)$ và $(BCD)$

b) Tìm giao điểm của mặt phẳng $(PMN)$ và $BC$.

Lời giải chi tiết

a) Trong $\left( {ABD} \right)$, ta có: $E = MP \cap BD$. Vì:

$\begin{array}{l} \left\{ \begin{array}{l} E \in BD \subset \left( {BCD} \right) \Rightarrow E \in \left( {BCD} \right)\\ E \in MP \subset \left( {MNP} \right) \Rightarrow E \in \left( {MNP} \right) \end{array} \right.\\ \Rightarrow E \in \left( {BCD} \right) \cap \left( {MNP} \right)\\ \text {Lại có:}\\ \left\{ \begin{array}{l} N \in CD \subset \left( {BCD} \right) \Rightarrow N \in \left( {BCD} \right)\\ N \in \left( {MNP} \right) \end{array} \right.\\ \Rightarrow N \in \left( {BCD} \right) \cap \left( {MNP} \right)\\ \Rightarrow NE = \left( {BCD} \right) \cap \left( {MNP} \right) \end{array}$ hay $NE$ là giao tuyến của mặt phẳng $BCD$ và $MNP$

b) Trong mặt phẳng $(BCD)$ gọi $Q$ là giao điểm của $NE$ và $BC$ ta có:

$\left\{ \begin{array}{l} Q \in BC\\ Q \in NE \subset \left( {MNP} \right) \Rightarrow Q \in \left( {MNP} \right) \end{array} \right.\\ \Rightarrow Q = BC \cap \left( {MNP} \right)$

HocTot.Nam.Name.Vn