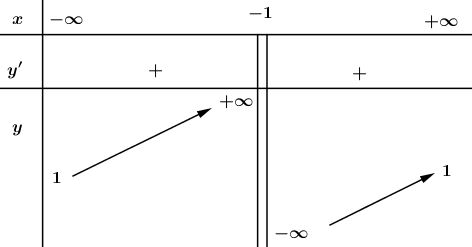
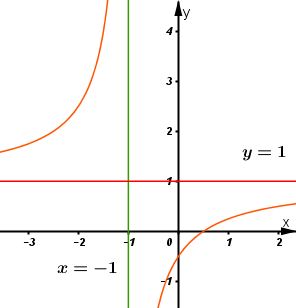
Giải bài 6 trang 44 SGK Giải tích 12

LG a

a) Chứng minh rằng với mọi giá trị của tham số \(m\), hàm số luôn đồng biến trên mỗi khoảng xác định của nó.

Phương pháp giải:

Tính đạo hàm của hàm số: \(y'\), chỉ ra \(y' > 0,\forall x \in D.\) 

Lời giải chi tiết:

\(\displaystyle y = {{mx - 1} \over {2x + m}}\).

Tập xác định: \(\displaystyle \mathbb R\backslash \left\{ {{{ - m} \over 2}} \right\}\)  ;

Ta có: \(\displaystyle y' = {{{m^2} + 2} \over {{{(2x + m)}^2}}} > 0,\forall x \ne  - {m \over 2}\)

  Do đó hàm số luôn đồng biến trên mỗi khoảng xác định của nó.

LG b

b) Xác định m để tiệm cận đứng đồ thị đi qua \(A(-1 ; \sqrt2)\).

Phương pháp giải:

Xác định đường tiệm cận của đồ thị hàm số theo m. Sau đó thế tọa độ của điểm A vào phương trình đường tiệm cận để tìm m.

Lời giải chi tiết:

Tiệm cận đứng \(\displaystyle ∆\): \(\displaystyle x =  - {m \over 2}\).

Vì \(\displaystyle A(-1 ; \sqrt2) ∈ ∆\) \(\displaystyle ⇔- {m \over 2}= -1 ⇔ m = 2\).

LG c

c) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi \(m = 2\).

Phương pháp giải:

Thay giá trị của m đã cho vào công thức hàm số sau đó khảo sát và vẽ đồ thị hàm số.

Lời giải chi tiết:

Với \(\displaystyle m = 2\) thì hàm số đã cho có phương trình là: \(\displaystyle y = {{2x - 1} \over {2x + 2}}\).

Tập xác đinh: \(\displaystyle D=\mathbb R\backslash {\rm{\{ }} - 1\} \)

* Sự biến thiên:

Ta có: \(\displaystyle y' = {2.2+2 \over {{{(2x + 2)}^2}}}={6 \over {{{(2x + 2)}^2}}} > 0\) \(\forall x \in D\)

- Hàm số đồng biến trên khoảng: \(\displaystyle (-\infty;-1)\) và \(\displaystyle (-1;+\infty)\)

- Cực trị:

   Hàm số không có cực trị.

- Tiệm cận:

   \(\displaystyle \eqalign{
& \mathop {\lim y}\limits_{x \to \pm \infty } = 1 \cr 
& \mathop {\lim y}\limits_{x \to - {1^ - }} = + \infty \cr 
& \mathop {\lim y}\limits_{x \to - {1^ + }} = - \infty \cr} \)

Tiệm cận đứng là \(\displaystyle x=-1\), tiệm cận ngang là: \(\displaystyle y=1\)

- Bảng biến thiên

* Đồ thị

Đồ thị hàm số giao \(\displaystyle Ox\) tại điểm \(\displaystyle ({1\over 2};0)\), giao \(\displaystyle Oy\) tại điểm \(\displaystyle (0;{-1\over 2})\).

Đồ thị hàm số nhận điểm \(\displaystyle I(-1;1)\) làm tâm đối xứng.

HocTot.Nam.Name.Vn