Bài 6. Phản xạ toàn phần Vở thực hành Khoa học tự nhiên 9Xét sự truyền sáng từ bán trụ thủy tinh ra không khí, khi góc tới bằng 41°, ta quan sát được đồng thời tia phản xạ và tia khúc xạ với góc khúc xạ với góc khúc xạ gần bằng 90° như hình bên. Theo em khi góc tới tiếp tục tăng lên tới giá trị 60° thì tia sáng sẽ truyền như thế nào? Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh
Lựa chọn câu để xem lời giải nhanh hơn
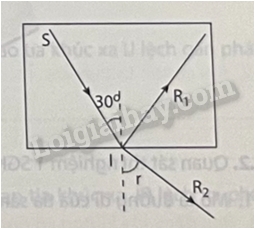
6.1 Xét sự truyền sáng từ bán trụ thủy tinh ra không khí, khi góc tới bằng 41°, ta quan sát được đồng thời tia phản xạ và tia khúc xạ với góc khúc xạ với góc khúc xạ gần bằng 90° như hình bên. Theo em khi góc tới tiếp tục tăng lên tới giá trị 60° thì tia sáng sẽ truyền như thế nào? Phương pháp giải: Phán đoán bằng kiến thức, kinh nghiệm, trải nghiệm của cá nhân Lời giải chi tiết: Khi góc tới tiếp tục tăng lên tới giá trị 60° thì ta sẽ thấy tia khúc xạ nhạt dần và biến mất, tia phản xạ đậm dần 6.2 1 Quan sát thí nghiệm về phản xạ toàn phần (Hình 6.1 SGK KHTN 9) và trả lời các câu hỏi sau: 1. Góc khúc xạ lớn hơn hay nhỏ hơn góc tới? Phương pháp giải: Quan sát thí nghiệm và trả lời câu hỏi Lời giải chi tiết: 1. Góc khúc xạ lớn hơn góc tới 6.2 2 2. Khi nào sẽ xảy ra hiện tượng chỉ có tia phản xạ? Phương pháp giải: Quan sát thí nghiệm và trả lời câu hỏi Lời giải chi tiết: 2. Khi chiếu góc tới bằng góc ith thì xảy ra hiện tượng chỉ có tia phản xạ 6.3 1 1. Tính góc tới hạn phản xạ toàn phần trong trường hợp tia sáng chiếu từ bản bán trụ thủy tinh (chiết suất n1 = 1,5) ra không khí (chiết suất n2 = 1). Phương pháp giải: 1. Áp dụng công thức tính ith: \(\sin {i_{th}} = \frac{{{n_2}}}{{{n_1}}}\) Lời giải chi tiết: 1. Góc tới hạn phản xạ toàn phần trong trường hợp chiếu từ bản bán trụ thủy tinh (chiết suất n1 = 1,5) ra không khí (chiết suất n2 = 1) là: \(\begin{array}{l}\sin {i_{th}} = \frac{{{n_2}}}{{{n_1}}} = \frac{1}{{1,5}} = \frac{2}{3}\\ \Rightarrow {i_{th}} = 41^\circ 48'\end{array}\) 6.3 2 2. Sử dụng dụng cụ thí nghiệm ở Hình 6.1 SGK KHTN 9 xác định giá trị ith, so sánh kết quả với câu 1 và rút ra nhận xét Phương pháp giải: 2. Làm lại thí nghiệm và quan sát góc tới hạn Lời giải chi tiết: 2. Sau khi thực hiện thí nghiệm ta có: ith ≈ 42° gần đúng với giá trị ở câu 1 Nhận xét: Khi góc tới lớn hơn hoặc bằng góc tới hạn thì toàn bộ tia sáng bị phản xạ ở mặt phân cách 6.4 Chiếu một tia sáng từ nước tới mặt phân cách giữa nước và không khí. Biết chiết suất của nước và không khí lần lượt là \({n_1} = \frac{4}{3},{n_2} = 1\) a) Tính góc khúc xạ trong trường hợp góc tới bằng 30° b) Khi góc tới bằng 60° thì có tia khúc xạ không? Tại sao? Phương pháp giải: Áp dụng công thức tính góc khúc xạ Lời giải chi tiết: a) Góc khúc xạ là: \(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}} \Leftrightarrow \frac{{\sin 30^\circ }}{{\sin r}} = \frac{1}{{\frac{4}{3}}} \Rightarrow \sin r = \frac{2}{3} \Rightarrow r = 41^\circ 48'\) b) Khi góc tới bằng 60° thì không còn tia khúc xạ vì đã xảy ra hiện tượng phản xạ toàn phần 6.5 Giải thích vì sao chỉ quan sát được hiện tượng ảo ảnh ở khoảng cách rất xa, khi lại gần thì không thấy nữa. Phương pháp giải: Vận dụng kiến thức về hiện tượng phản xạ toàn phần Lời giải chi tiết: Nguyên nhân vật lý là trong điều kiện sa mạc hay đường nhựa nóng, không khí tại gần mặt đất có nhiệt độ cao hơn không khí trên cao, dẫn đến chiết suất không khí tăng theo độ cao. Trong điều kiện này, các tia sáng từ bầu trời xanh có thể được phản xạ toàn phần đến mắt người quan sát 6.6 1 1. Giải thích sự truyền ánh sáng trong sợi quang Phương pháp giải: Vận dụng kiến thức về phản xạ toàn phần Lời giải chi tiết: 1. Ánh sáng trong cáp sợi quang truyền qua lõi và va đập liên tục vào lớp sơn phủ. Bởi vì lớp sơn phủ không hấp thu bất kì ánh sáng trong lõi nên sóng ánh sáng có thể truyền đi với cự li rất xa. Tuy nhiên ánh sáng cũng có thể bị giảm sút bởi sự không tinh khiến của thủy tinh. Sự suy giảm tín hiệu phụ thuộc vào độ tinh khiến của thủy tinh. 6.6 2 2. Nêu một số ứng dụng của sợi quang trong y học, công nghệ thông tin Phương pháp giải: Vận dụng kiến thức về phản xạ toàn phần Lời giải chi tiết: 2. Ứng dụng: - Trong y học: Đây là một lĩnh vực mà có ý nghĩa rất lớn đối với con người chúng ta ảnh hưởng trực tiếp đến cuộc sống của chúng ta hàng ngày và cáp quang được sử dụng rộng rãi trong lĩnh vực này mang đến những phương thức phẫu thuật hiệu quả không xâm nhập vào cơ thể người đó là phương pháo nội soi ánh sáng chói lóa của sợi quang được sử dụng để soi sáng vùng phẫu thuật bên trong cơ thể, giúp giảm kích thước của vết rạch, đây là bước ngoặt rất lớn trong công nghệ cáp quang đối với y tế. - Trong công nhệ thông tin: Mạng cáp quang nối nhiều quốc gia trên thế giới liên kết người dùng với nhau. Mạng quang riêng của các công ty đường sắt, điện lực, bộ ngành …. Đường cáp quang trung kế ,đường cáp quang thả biển xuyên quốc gia. Đường cáp quang truyền số liệu, mạng LAN, mạng nội bộ. Mạng cáp quang truyền hình, internet kết nối nhỏ lẻ đến tận từng các hộ gia đình. 6.7 Nêu điều kiện để xảy ra hiện tượng phản xạ toàn phần. Phương pháp giải: Vận dụng kiến thức về phản xạ toàn phần Lời giải chi tiết: Điều kiện để có phản xạ toàn phần - Ánh sáng truyền từ môi trường có chiết suất n1 tới môi trường có chiết suất n2 với \({n_1} > {n_2}\) - Góc tới lớn hơn hoặc bằng góc tới hạn: \(i \ge {i_{gh}}\) 6.8 Một chùm sáng hẹp truyền từ thủy tinh có chiết suất n = 1,5 đến mặt phân cách với môi trường khác có chiết suất n. Để tia tới gặp mặt phân cách giữa hai môi trường dưới góc i ≥ 50° sẽ xảy ra hiện tượng phản xạ toàn phần thì chiết suất n' phải thỏa mãn điều kiện gì? Phương pháp giải: Vận dụng kiến thức về phản xạ toàn phần Lời giải chi tiết: Hiện tượng phản xạ toàn phần xảy ra khi tia sáng đi từ môi trường có chiết suất lớn hơn đến môi trường có chiết suất nhỏ hơn và góc tới lớn hơn góc giới hạn phản xạ toàn phần. Cho chiết suất của thủy tinh là \({n_1} = 1,5\) và chiết suất của môi trường thứ hai là \({n_2} = n\). Để xảy ra hiện tượng phản xạ toàn phần, góc tới \(i \ge 50^\circ \) ta có công thức tính góc giới hạn phản xạ toàn phần: \(\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}}\) Với điều kiện \({i_{gh}} \le {50^ \circ }\)ta có: \(\sin {50^ \circ } \ge \frac{n}{{1,5}}\) Từ đó suy ra: \(n \le 1.5\sin {50^ \circ }\) \( \Rightarrow n \le 1,5.0,766 = 1,149\) 6.9 Một tia sáng truyền trong thuỷ tinh đến mặt phân cách giữa thủy tinh với không khí tại điểm I với góc tới i = 30° thì tia phản xạ và tia khúc xạ vuông góc nhau. Tính chiết suất của thuỷ tinh. Phương pháp giải: Vận dụng kiến thức về phản xạ toàn phần Lời giải chi tiết: Do tia phản xạ và tia khúc xạ vuông góc nhau, nên góc khúc xạ r thỏa mãn: \(i + r = 90^\circ \Rightarrow r = 90^\circ - i = 90^\circ - 30^\circ = 60^\circ \) Ta có: \({n_1}\sin i = {n_2}\sin r \Rightarrow n.\sin 30^\circ = 1.\sin 60^\circ \Rightarrow n = \sqrt 3 \) 6.10 Có ba môi trường trong suốt (1), (2) và (3). Với cùng một góc tới, nếu ánh sáng đi từ môi trường (1) vào môi trường (2) thì góc khúc xạ là 30°, nếu ánh sáng đi từ môi trường (1) vào môi trường (3) thì góc khúc xạ là 45°. a) Trong hai môi trường (2) và (3), chiết suất của môi trường nào lớn hơn? b) Tính góc tới hạn phản xạ toàn phần giữa hai môi trường (2) và (3). Phương pháp giải: Vận dụng kiến thức về phản xạ toàn phần Lời giải chi tiết: a) Ta có: \(\begin{array}{l}{n_1}\sin i = {n_2}\sin {r_2}\\{n_1}\sin i = {n_3}\sin {r_3}\\ \Rightarrow {n_2}\sin {r_2} = {n_3}\sin {r_3}\\ \Rightarrow \frac{{{n_2}}}{{{n_3}}} = \frac{{\sin {r_3}}}{{\sin {r_2}}} = \frac{{\sin 45^\circ }}{{\sin 30^\circ }} = \sqrt 2 \\ \Rightarrow {n_2} = \sqrt 2 {n_3}\end{array}\) Chiết suất của môi trường (2) lớn hơn chiết suất của môi trường (3) b) Góc tới hạn giữa hai môi trường được xác định bằng công thức: \(\begin{array}{l}\sin {i_{gh}} = \frac{{{n_3}}}{{{n_2}}} = \frac{{{n_3}}}{{\sqrt 2 {n_3}}} = \frac{1}{{\sqrt 2 }}\\ \Rightarrow {i_{gh}} = 45^\circ \end{array}\) Vậy, góc tới hạn phản xạ toàn phần giữa hai môi trường (2) và (3) là 45°
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|