Bài 5 trang 83 SGK Đại số và Giải tích 11

Video hướng dẫn giải

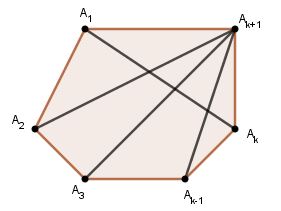Vậy số đường chéo của đa giác $k + 1$ cạnh là

$\displaystyle {{k(k - 3)} \over 2}+ k - 2 + 1$

$= \dfrac{{{k^2} - 3k}}{2} + k - 1$

$= \dfrac{{{k^2} - 3k + 2k - 2}}{2}$

$\displaystyle ={{{k^2} - k - 2} \over 2}$

$= \dfrac{{\left( {k + 1} \right)\left( {k - 2} \right)}}{2}$

$\displaystyle = {{(k + 1)((k + 1) - 3)} \over 2}$

Như vậy, khẳng định cũng đúng với đa giác $k + 1$ cạnh

Vậy bài toán đã được chứng minh.

Chú ý:

Trên đây là cách chứng minh bằng quy nạp, các em có thể dễ dàng chứng minhcông thức đó bằng kiến thức chương 2 như sau:

Cách 2: Đa giác lồi $n$ cạnh có $n$ đỉnh.

Chọn 2 điểm bất kì trong số các đỉnh của một đa giác ta được 1 cạnh hoặc 1 đường chéo của đa giác.

⇒ Tổng số cạnh và đường chéo của đa giác bằng:

$C_n^2 = \dfrac{{n!}}{{2!\left( {n - 2} \right)!}}$$= \dfrac{{n\left( {n - 1} \right)\left( {n - 2} \right)!}}{{2\left( {n - 2} \right)!}} = \dfrac{{n\left( {n - 1} \right)}}{2}$

⇒ Số đường chéo của đa giác lồi có $n$ cạnh là:

$\dfrac{{n\left( {n - 1} \right)}}{2} - n = \dfrac{{{n^2} - n - 2n}}{2}$$= \dfrac{{{n^2} - 3n}}{2} = \dfrac{{n\left( {n - 3} \right)}}{2}$

Vậy ta có đpcm.

HocTot.Nam.Name.Vn