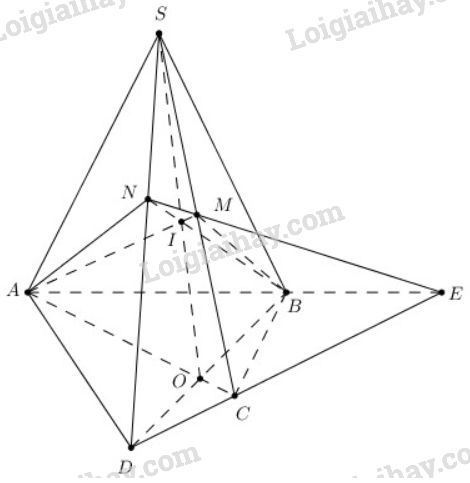
Bài 5 trang 53 SGK Hình học 11

Đề bài

Cho tứ giác $ABCD$ nằm trong mặt phẳng $(α)$ có hai cạnh $AB$ và $CD$ không song song. Gọi $S$ là điểm nằm ngoài mặt phẳng $(α)$ và $M$ là trung điểm đoạn $SC$.

a) Tìm giao điểm $N$ của đường thẳng $SD$ và mặt phẳng $(MAB)$.

b) Gọi $O$ là giao điểm của $AC$ và $BD$. Chứng minh rằng ba đường thẳng $SO, AM, BN$ đồng quy.

Lời giải chi tiết

a) Trong mặt phẳng $(α)$ vì $AB$ và $CD$ không song song nên $AB ∩ DC = E$

$\Rightarrow E ∈ DC$, mà $DC ⊂ (SDC)$

$\Rightarrow E ∈ ( SDC)$.

Trong $(SDC)$ đường thẳng $ME$ cắt $SD$ tại $N$

$\Rightarrow N ∈ ME$ mà $ME ⊂ (MAB)$

$\Rightarrow N ∈ ( MAB)$. Lại có $N ∈ SD \Rightarrow N = SD ∩ (MAB)$

b) $O$ là giao điểm của $AC$ và $BD$$\Rightarrow O$ thuộc $AC$ và $BD$, mà $AC ⊂ ( SAC), BD ⊂ (SBD)$

$\Rightarrow O ∈( SAC), O ∈ (SBD)$

$\Rightarrow$  $O$ là một điểm chung của $(SAC)$ và $(SBD)$

Mặt khác $S$ cũng là điểm chung của $(SAC)$ và $(SBD)$

$\Rightarrow  (SAC) ∩ (SBD) = SO$

Trong mặt phẳng $(AEN)$ gọi $I = AM ∩ BN \Rightarrow I \in AM; I \in BN$

Mà $AM ⊂ (SAC) \Rightarrow  I ∈ (SAC)$

$BN ⊂ ( SBD)$$\Rightarrow  I ∈ (SBD)$.

Như vậy $I$ là điểm chung của $(SAC)$ và $(SBD)$ nên $I \in SO$ là giao tuyến của $(SAC)$ và $(SBD)$.

Vậy $S, I, O$ thẳng hàng hay $SO, AM, BN$ đồng quy tại $I$.

Cách khác:

b) Chứng minh $SO, MA, BN$ đồng quy:

+ Trong mặt phẳng $(SAC) : SO$ và $AM$ cắt nhau.

+ Trong mp $(MAB) : MA$ và $BN$ cắt nhau

+ Trong mp $(SBD) : SO$ và $BN$ cắt nhau.

+ Qua $AM$ và $BN$ xác định được duy nhất $(MAB)$, mà $SO$ không nằm trong mặt phẳng $(MAB)$ nên $AM; BN; SO$ không đồng phẳng.

Theo kết quả bài tập 3 ta có $SO, MA, BN$ đồng quy.

HocTot.Nam.Name.Vn