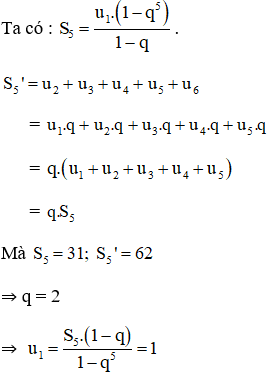Bài 4 trang 104 SGK Đại số và Giải tích 11Tìm cấp số nhân có sau số hạng, biết rằng tổng của năm số hạng đầu là 31 và tổng của năm số hạng sau là 62. Đề bài Tìm cấp số nhân có sáu số hạng, biết rằng tổng của năm số hạng đầu là và tổng của năm số hạng sau là . Video hướng dẫn giải Phương pháp giải - Xem chi tiết Sử dụng công thức số hạng tổng quát của CSN: và công thức tổng n số hạng đầu tiên của CSN: . Lời giải chi tiết Giả sử có cấp số nhân: Theo giả thiết ta có: . (1) . (2) Nhân hai vế của (1) với , ta được: (3) Từ (2) và (3) . Ta có Vậy ta có cấp số nhân là: . Cách khác:
Vậy ta có cấp số nhân là: . HocTot.Nam.Name.Vn
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|