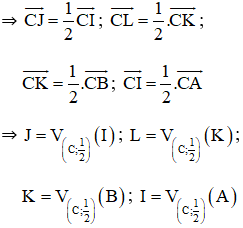Bài 2 trang 33 SGK Hình học 11Cho hình chữ nhật ABCD, AC và BD cắt nhau tại I. Gọi H, K, L và J lần lượt là trung điểm của AD, BC, KC và IC. Đề bài Cho hình chữ nhật và cắt nhau tại . Gọi và lần lượt là trung điểm của và . Chứng minh hai hình thang và đồng dạng với nhau. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Thực hiện liên tiếp hai phép biến hình sau: - Phép vị tự tâm tỉ số - Phép đối xứng tâm Lời giải chi tiết
Ta có: là trung điểm của nên
Do đó . Lại có, Nên . Do đó tồn tại phép đồng dạng (hợp bởi phép vị tự và phép đối xứng tâm) biến hình thang thành hình thang . Vậy hai hình thang và hình thang đồng dạng. Cách khác: + là trung điểm
Hình thang đối xứng với hình thang qua (1) + lần lượt là trung điểm của Hình thang là ảnh của hình thang qua phép vị tự tâm tỉ số Hình thang là ảnh của hình thang qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng tâm và phép vị tự tâm tỉ số . và đồng dạng. HocTot.Nam.Name.Vn
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|