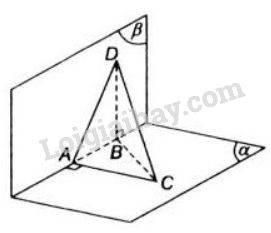
Bài 2 trang 113 SGK Hình học 11

Đề bài

Cho hai mặt phẳng $(\alpha)$ và $(\beta)$ vuông góc với nhau. Người ta lấy trên giao tuyến $\Delta$ của hai mặt phẳng đó hai điểm $A$ và $B$ sao cho $AB=8cm$. Gọi $C$ là một điểm trên $(\alpha)$ và $D$ là một điểm trên $(\beta)$ sao cho $AC$ và $BD$ cùng vuông góc với giao tuyến $\Delta$ và $AC=6cm$, $BD=24cm$. Tính độ dài đoạn $CD$.

Lời giải chi tiết

$\left. \matrix{(\alpha ) \bot (\beta ) \hfill \cr AC \bot \Delta \hfill \cr AC \subset (\alpha ) \hfill \cr} \right\} \Rightarrow AC \bot (\beta )$

Do đó $AC\bot AD$ hay tam giác $ACD$ vuông tại $A$

Áp dụng định lí Pytago vào tam giác $ACD$ ta được: $D{C^2} = A{C^2} + A{D^2}(1)$

Vì $BD\bot AB \Rightarrow \Delta ABD$ vuông tại $B$.

Áp dụng định lí Pytago vào tam giác $ABD$ ta được: $A{D^2} = A{B^2} + B{D^2}(2)$

Từ (1) và (2) suy ra: $D{C^2} = A{C^2} + A{B^2} + B{D^2} = {6^2} + {8^2} + {24^2} = 676$

$\Rightarrow DC = \sqrt {676}  = 26cm$

 HocTot.Nam.Name.Vn