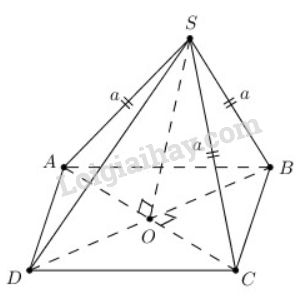
Bài 6 trang 114 SGK Hình học 11Cho hình chóp S.ABCD có đáy ABCD là một hình thoi cạnh a và có SA = SB = SC = a... Đề bài Cho hình chóp S.ABCDS.ABCD có đáy ABCDABCD là một hình thoi cạnh aa và có SA=SB=SC=aSA=SB=SC=a. Chứng minh rằng: a) Mặt phẳng (ABCD)(ABCD) vuông góc với mặt phẳng (SBD)(SBD); b) Tam giác SBDSBD là tam giác vuông. Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Chứng minh AC⊥(SBD)AC⊥(SBD). b) Chứng minh tam giác SBDSBD có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó. Lời giải chi tiết
a) Gọi OO là giao điểm của hai đường chéo ACAC và BDBD Theo tính chất của hình thoi thì OO là trung điểm của AC,BDAC,BD Xét tam giác cân SACSAC cân tại SS ta có: SOSO vừa là đường trung tuyến đồng thời là đường cao do đó SO⊥ACSO⊥AC (1) Mặt khác ABCDABCD là hình thoi nên AC⊥BDAC⊥BD (2) Từ (1) và (2) suy ra AC⊥(SBD)AC⊥(SBD) AC⊂(ABCD)⇒(ABCD)⊥(SBD)AC⊂(ABCD)⇒(ABCD)⊥(SBD) b) ∆SAC=∆BAC(c.c.c)ΔSAC=ΔBAC(c.c.c) Do đó các đường trung tuyến ứng với các đỉnh tương ứng của hai tam giác bằng nhau: SO=BOSO=BO OO là trung điểm của BDBD nên OB=ODOB=OD ⇒SO=BO=12BD⇒SO=BO=12BD Tam giác SBDSBD có trung tuyển SO=12BDSO=12BD nên vuông tại SS. (đpcm) Cách khác: Tam giác SOCSOC vuông tại OO nên theo Pi-ta-go ta có: SO2=SC2−OC2=a2−OC2SO2=SC2−OC2=a2−OC2 Tam giác BOCBOC vuông tại OO nên theo Pi-ta-go ta có: BO2=BC2−OC2=a2−OC2BO2=BC2−OC2=a2−OC2 ⇒SO=BO=12BD⇒SO=BO=12BD Tam giác SBDSBD có trung tuyển SO=12BDSO=12BD nên vuông tại SS. (đpcm) HocTot.Nam.Name.Vn
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|