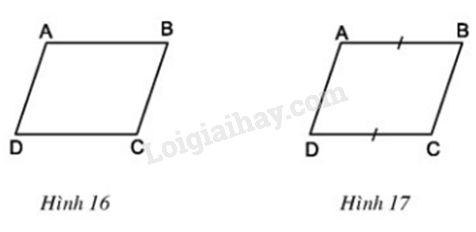
Trả lời câu hỏi 2 Bài 2 trang 70 SGK Toán 8 Tập 1

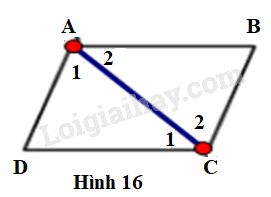
LG a.

Cho biết $AD // BC$ (h.16). Chứng minh rằng $AD = BC, AB = CD.$

Phương pháp giải:

Áp dụng:

- Xét hai tam giác bằng nhau

- Hai đường thẳng song song thì có cặp góc so le trong bằng nhau.

Lời giải chi tiết:

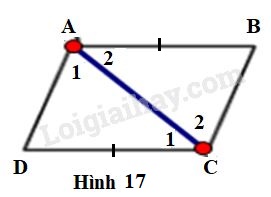
Hình thang $ABCD$ có đáy $AB,\,\,CD \Rightarrow AB//CD \Rightarrow \widehat {{A_2}} = \widehat {{C_1}}$ (hai góc so le trong) 

Lại có: $AD // BC$ $\Rightarrow \widehat {{A_1}} = \widehat {{C_2}}$ (hai góc so le trong)

Xét $ΔABC$ và $ΔCDA$ có:

+) $\widehat {{A_2}} = \widehat {{C_1}}$ (chứng minh trên)

+) $AC$ chung

+) $\widehat {{A_1}} = \widehat {{C_2}}$ (chứng minh trên)

$\Rightarrow  ΔABC = ΔCDA$ (g.c.g)

$\Rightarrow  AD = BC, AB = CD$ (các cặp cạnh tương ứng)

LG b.

Cho biết $AB = CD$ (h.17). Chứng minh rằng $AD // BC, AD = BC.$

Phương pháp giải:

Áp dụng:

- Xét hai tam giác bằng nhau

- Hai đường thẳng song song nếu có cặp góc so le trong bằng nhau.

Lời giải chi tiết:

Hình thang $ABCD$ có đáy $AB,\,\,CD \Rightarrow AB//CD \Rightarrow \widehat {{A_2}} = \widehat {{C_1}}$ (hai góc so le trong) 

Xét $ΔABC$ và $ΔCDA$ có:

+) $AC$ chung

+) $\widehat {{A_2}} = \widehat {{C_1}}$  (chứng minh trên)

+) $AB = CD$ (giả thiết)

$\Rightarrow  ΔABC = ΔCDA$ (c.g.c)

$\Rightarrow  AD = BC$ (hai cạnh tương ứng)

$\widehat {{A_1}} = \widehat {{C_2}}$ (hai góc tương ứng)

Mặt khác $\widehat {{A_1}} ;\, \widehat {{C_2}}$ ở vị trí so le trong.

$\Rightarrow  AD // BC$ ( Dấu hiệu nhận biết 2 đường thẳng song song)