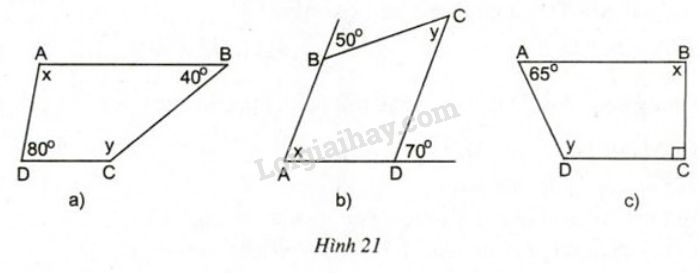
Bài 7 trang 71 SGK Toán 8 tập 1Tìm x và y trên hình 21, biết rằng ABCD là hình thang có đáy Đề bài Tìm x và y trên hình 21, biết rằng ABCD là hình thang có đáy là AB và CD.
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng các tính chất của một đường thẳng cắt hai đường thẳng song song: hai góc trong cùng phía bù nhau, hai góc đồng vị bằng nhau, hai góc so le trong bằng nhau. Lời giải chi tiết Vì ABCD là hình thang có đáy là AB và CD nên AB//CD a) Ta có: AB//DC (chứng minh trên) ⇒ˆA+ˆD=1800 (hai góc trong cùng phía bù nhau) ⇒x+800=1800 ⇒x=1800−800=1000 Ta có: AB//DC (chứng minh trên) ⇒ˆC+ˆB=1800 (hai góc trong cùng phía bù nhau) ⇒y+400=1800 ⇒y=1800−400=1400 b) Vì AB//DC (chứng minh trên) ⇒x=700 (hai góc đồng vị bằng nhau) ⇒y=500 (hai góc so le trong bằng nhau) c) Ta có AB//DC (chứng minh trên) ⇒ˆB+ˆC=1800 (hai góc trong cùng phía bù nhau) ⇒x+900=1800 ⇒x=1800−900=900 Ta có AB//DC (chứng minh trên) ⇒ˆD+ˆA=1800 (hai góc trong cùng phía bù nhau) ⇒y+650=1800 ⇒y=1800−650=1150 HocTot.Nam.Name.Vn
|