Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo

Lý thuyết Tích phân Toán 12 Chân trời sáng tạo

1. Diện tích hình thang cong

Gửi góp ý cho HocTot.Nam.Name.Vn và nhận về những phần quà hấp dẫn

1. Diện tích hình thang cong

Nếu hàm số f(x) liên tục và không âm trên đoạn

$\left[ {a;b} \right]$ , thì diện tích S của hình thang cong giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b là S = F(b) – F(a), trong đó F(x) là một nguyên hàm của hàm số f(x) trên

$\left[ {a;b} \right]$ .

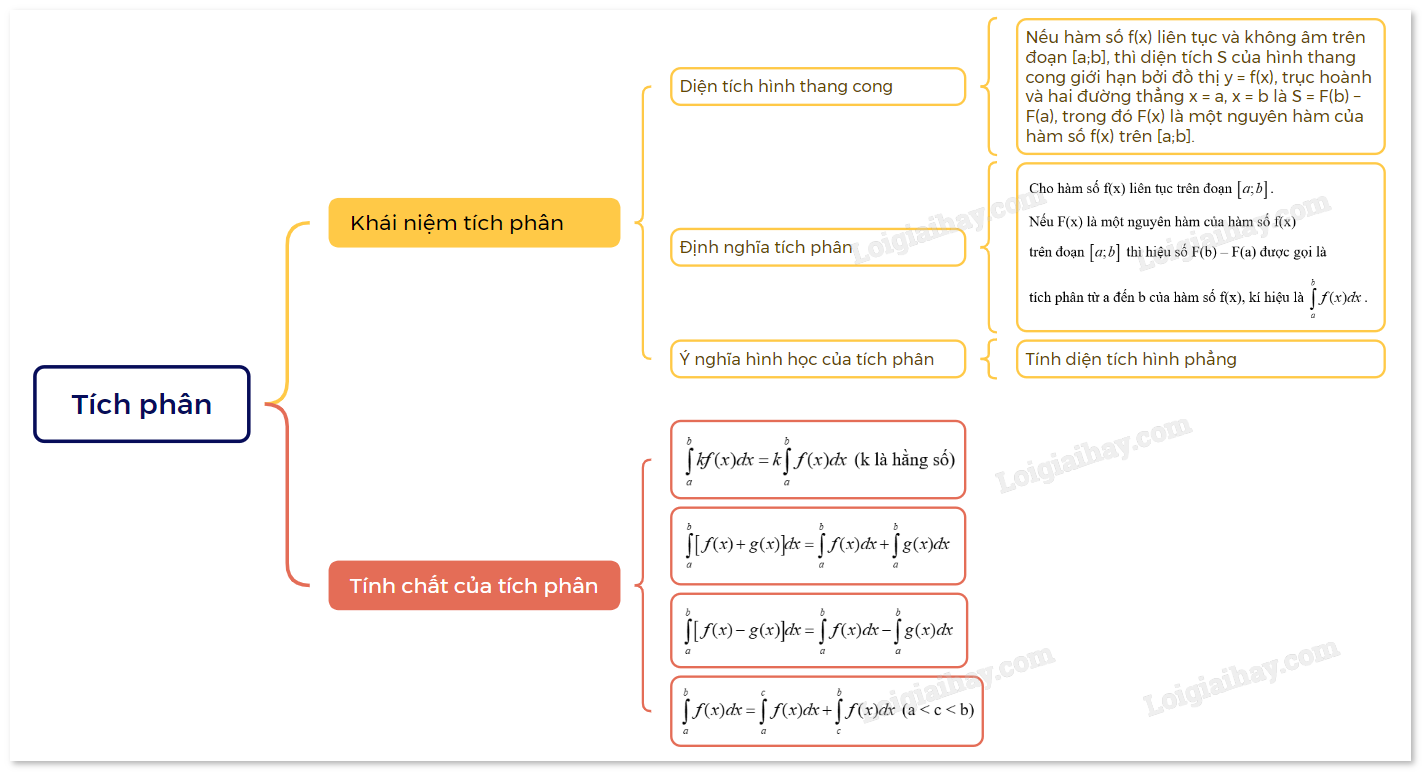
2. Khái niệm tích phân

Cho hàm số f(x) liên tục trên đoạn

$\left[ {a;b} \right]$ . Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn

$\left[ {a;b} \right]$ thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là

$\int\limits_a^b {f(x)dx}$ .

Chú ý:

a) Trong trường hợp a = b hoặc a > b, ta quy ước

$\int\limits_a^a {f(x)dx = 0}$ và $\int\limits_a^b {f(x)dx} = - \int\limits_b^a {f(x)dx}$

b) Người ta chứng minh được, tích phân chỉ phụ thuộc vào hàm số f và các cận a, b mà không phụ thuộc vào biến số x hay t, nghĩa là $\int\limits_a^b {f(x)dx = \int\limits_a^b {f(t)dt} }$

c) Ý nghĩa hình học của tích phân: Nếu hàm số f(x) liên tục và không âm trên đoạn $\left[ {a;b} \right]$ , thì tích phân $\int\limits_a^b {f(x)dx}$ là diện tích S của hình thang cong giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b

3. Tính chất của tích phân

+ $\int\limits_a^b {kf(x)dx = k\int\limits_a^b {f(x)dx} }$ (k là hằng số)

+ $\int\limits_a^b {\left[ {f(x) + g(x)} \right]} dx = \int\limits_a^b {f(x)dx + \int\limits_a^b {g(x)dx} }$

+ $\int\limits_a^b {\left[ {f(x) - g(x)} \right]} dx = \int\limits_a^b {f(x)dx - \int\limits_a^b {g(x)dx} }$

+ $\int\limits_a^b {f(x)dx = \int\limits_a^c {f(x)dx + \int\limits_c^b {f(x)dx} } }$ (a < c < b)

Chia sẻ

Bình luận

Bình chọn:

3.8 trên 4 phiếu

Giải câu hỏi mở đầu trang 12 SGK Toán 12 tập 2 - Chân trời sáng tạo
Khi được thả từ độ cao 20 m, một vật rơi với gia tốc không đổi a = 10 $m/{s^2}$ . Sau khi rơi được t giây thì vật có tốc độ bao nhiêu và đi được quãng đường bao nhiêu?
Giải mục 1 trang 12, 13 SGK Toán 12 tập 2 - Chân trời sáng tạo
Diện tích hình thang cong
Giải mục 2 trang 14,15,16 SGK Toán 12 tập 2 - Chân trời sáng tạo
Khái niệm tích phân
Giải mục 3 trang 16,17,18 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tính chất của tích phân
Giải bài tập 1 trang 20 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tính diện tích hình thang cong giới hạn bởi: a) Đồ thị hàm số (y = {x^2}), trục hoành và hai đường thẳng (x = 0), (x = 2). b) Đồ thị hàm số (y = frac{1}{x}), trục hoành và hai đường thẳng (x = 1), (x = 3).

Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.