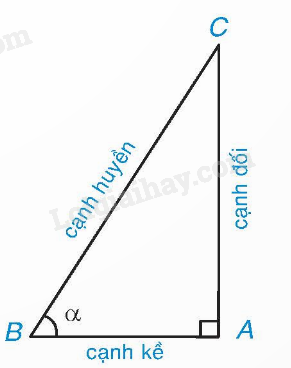
Lý thuyết Tỉ số lượng giác của góc nhọn Toán 9 Cánh diều1. Tỉ số lượng giác của một góc nhọn sinα=cạnhđốicạnhhuyền;cosα=cạnhkềcạnhhuyền; tanα=cạnhđốicạnhkề;cotα=cạnhkềcạnhđối. cotα=1tanα. sinα,cosα,tanα,cotα gọi là các tỉ số lượng giác của góc nhọn α. Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh 1. Tỉ số lượng giác của một góc nhọn
Tip học thuộc nhanh:
Ví dụ:
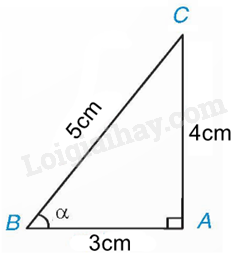
Theo định nghĩa của tỉ số lượng giác, ta có: sinα=ACBC=45, cosα=ABBC=35, tanα=ACAB=43, cotα=ABAC=34 2. Tỉ số lượng giác của hai góc phụ nhau Nhận xét: Hai góc nhọn có tổng bằng 900 được gọi là hai góc phụ nhau. Định lí về tỉ số lượng giác của hai góc phụ nhau
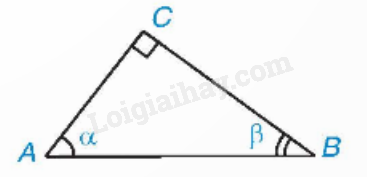
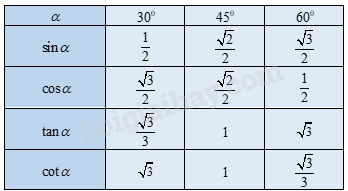
Cho α và β là hai góc phụ nhau, ta có: sinα=cosβ, cosα=sinβ, tanα=cotβ, cotα=tanβ. Ví dụ: sin600=cos(900−600)=cos300;cos52030′=sin(900−52030′)=sin37030′;tan800=cot(900−800)=cot100;cot820=tan(900−820)=tan80. Bảng giá trị lượng giác của các góc 300,450,600
Quy ước: sin2α=(sinα)2;cos2α=(cosα)2;tan2α=(tanα)2;cot2α=(cotα)2. 3. Sử dụng máy tính cầm tay tính tỉ số lượng giác của một góc nhọn Người ta thường dùng các đơn vị số đo góc là độ (kí hiệu: 0), phút (kí hiệu: ′), giây (kí hiệu: ″). Ta có thể sử dụng nhiều loại máy tính cầm tay để tính các tỉ số lượng giác của góc nhọn và tính số đo của góc nhọn khi biết một tỉ số lượng giác của nó. Lưu ý: ta cần đổi đơn vị đo về độ.
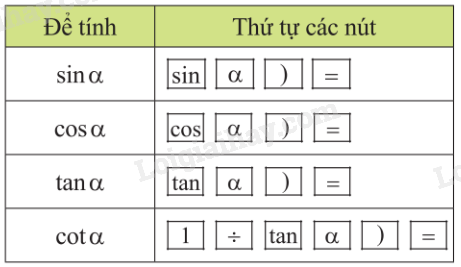
Tính các tỉ số lượng giác của các góc nhọn Để tính tỉ số lượng giác của một góc α, ta dùng các nút:
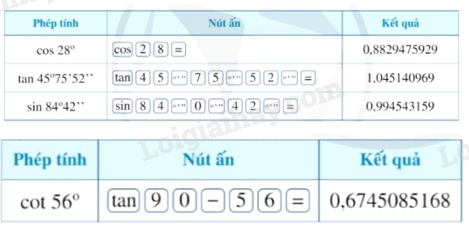
Để tính cotα, ta tính cotα=1tanα hoặc tan(900−α). Bảng tóm tắt cách tính tỉ số lượng giác của một góc nhọn
Ví dụ:
Xác định số đo của góc nhọn khi biết một tỉ số lượng giác của góc đó Bảng tóm tắt cách tính số đo của một góc nhọn khi biết một tỉ số lượng giác
Để tìm α khi biết cotα, ta tính tanα=1cotα và dùng tanα để tính α. Ví dụ:
Một số công thức mở rộng: +) sin2α+cos2α=1 +) tanα=sinαcosα +) cotα=cosαsinα +) tanα.cotα=1 +) 1cos2α=tan2α+1 +) 1sin2α=cot2α+1 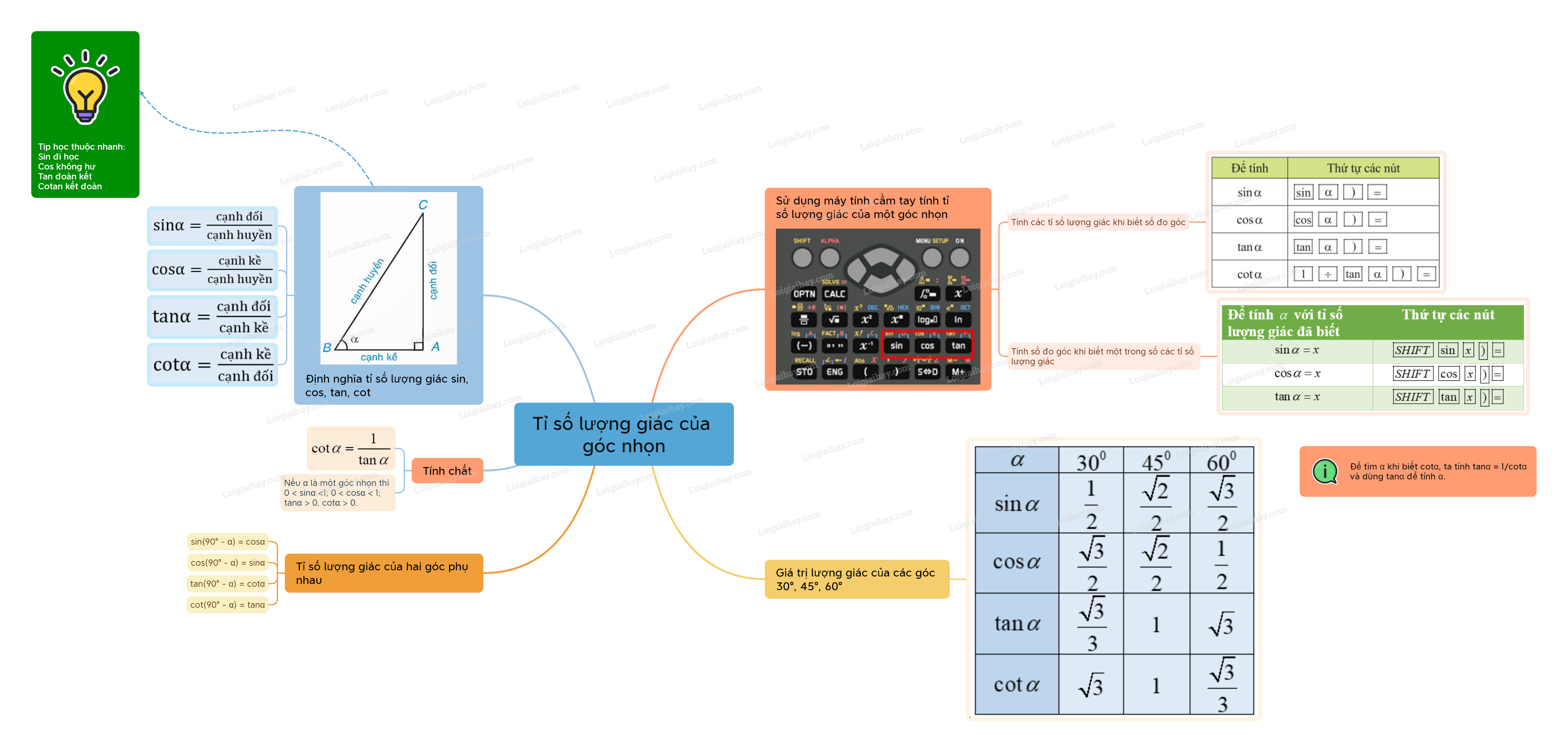
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|