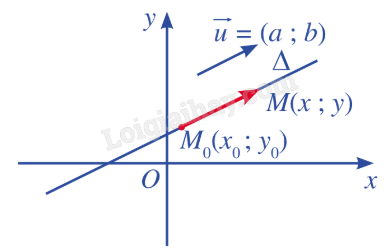
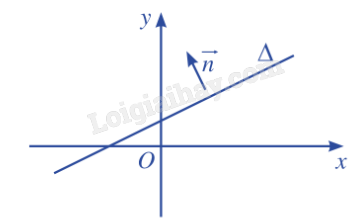
Lý thuyết Phương trình đường thẳng - SGK Toán 10 Cánh diều

A. Lý thuyết

1. Phương trình tham số của đường thẳng

a) Vecto chỉ phương của đường thẳng

Nhận xét:

- Nếu \(\overrightarrow u \) là một vecto chỉ phương của \(\Delta \) thì \(k\overrightarrow u \) \((k \ne 0)\) cũng là một vecto chỉ phương của \(\Delta \).

- Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vecto chỉ phương của đường thẳng đó.

b) Phương trình tham số của đường thẳng

Với mỗi giá trị cụ thể của t, ta xác định được một điểm trên đường thẳng \(\Delta \). Ngược lại, với mỗi điểm trên đường thẳng \(\Delta \), ta xác định được một giá trị cụ thể của t.

2. Phương trình tổng quát của đường thẳng

a) Vecto pháp tuyến của đường thẳng

Nhận xét:

- Nếu \(\overrightarrow n \) là một vecto pháp tuyến của \(\Delta \) thì \(k\overrightarrow n \) \((k \ne 0)\) cũng là một vecto pháp tuyến của \(\Delta \).

- Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vecto pháp tuyến của đường thẳng đó.

b) Phương trình tổng quát của đường thẳng

Nhận xét:

- Đường thẳng \(\Delta \) đi qua \({M_0}({x_0};{y_0})\) và nhận \(\overrightarrow n  = (a;b)\) làm vecto pháp tuyến có phương trình là \(a(x - {x_0}) + b(y - {y_0}) = 0 \Leftrightarrow ax + by + ( - a{x_0} - b{y_0}) = 0\).

- Mỗi phương trình \(ax + by + c = 0\) (a và b không đồng thời bằng 0)  đều xác định một đường thẳng \(\Delta \) trong mặt phẳng tọa độ nhận một vecto pháp tuyến là \(\overrightarrow n  = (a;b)\).

c) Những dạng đặc biệt của phương trình tổng quát

- Đường thẳng \(\Delta \) có phương trình tổng quát \(ax + by + c = 0\) (a hoặc b khác 0) là đồ thị hàm số bậc nhất khi và chỉ khi \(a \ne 0\) và \(b \ne 0\).

- Phương trình trục hoành là y = 0, phương trình trục tung là x = 0.

3. Lập phương trình đường thẳng

Khi lập phương trình đường thẳng, ta thường gặp ba trường hợp như sau:

– Đi qua một điểm cho trước và biết vecto pháp tuyến.

– Đi qua một điểm cho trước và biết vecto chỉ phương.

– Đi qua hai điểm cho trước.

a) Lập phương trình đường thẳng đi qua một điểm và biết vecto pháp tuyến

b) Lập phương trình đường thẳng đi qua một điểm và biết vecto chỉ phương

c) Lập phương trình đường thẳng đi qua hai điểm

4. Phương trình đoạn chắn

B. Bài tập

Lập phương trình đường thẳng \(\Delta \) thỏa mãn:

a) Đi qua M(-2;-3) và có \(\overrightarrow n  = (2;5)\) là vecto pháp tuyến.

b) Đi qua M(3;-5) và có \(\overrightarrow u  = (2; - 4)\) là vecto chỉ phương.

c) Đi qua A(-3;4) và B(1;-1).

Giải:

a) Phương trình \(\Delta \) là \(2(x + 2) + 5(y + 3) = 0 \Leftrightarrow 2x + 5y + 19 = 0\).

b) Phương trình \(\Delta \) là \(\frac{{x - 3}}{2} = \frac{{y + 5}}{{ - 4}} \Leftrightarrow 4x + 2y - 2 = 0 \Leftrightarrow 2x + y - 1 = 0\).

c) Phương trình \(\Delta \) là \(\frac{{x + 3}}{{1 - ( - 3)}} = \frac{{y - 4}}{{ - 1 - 4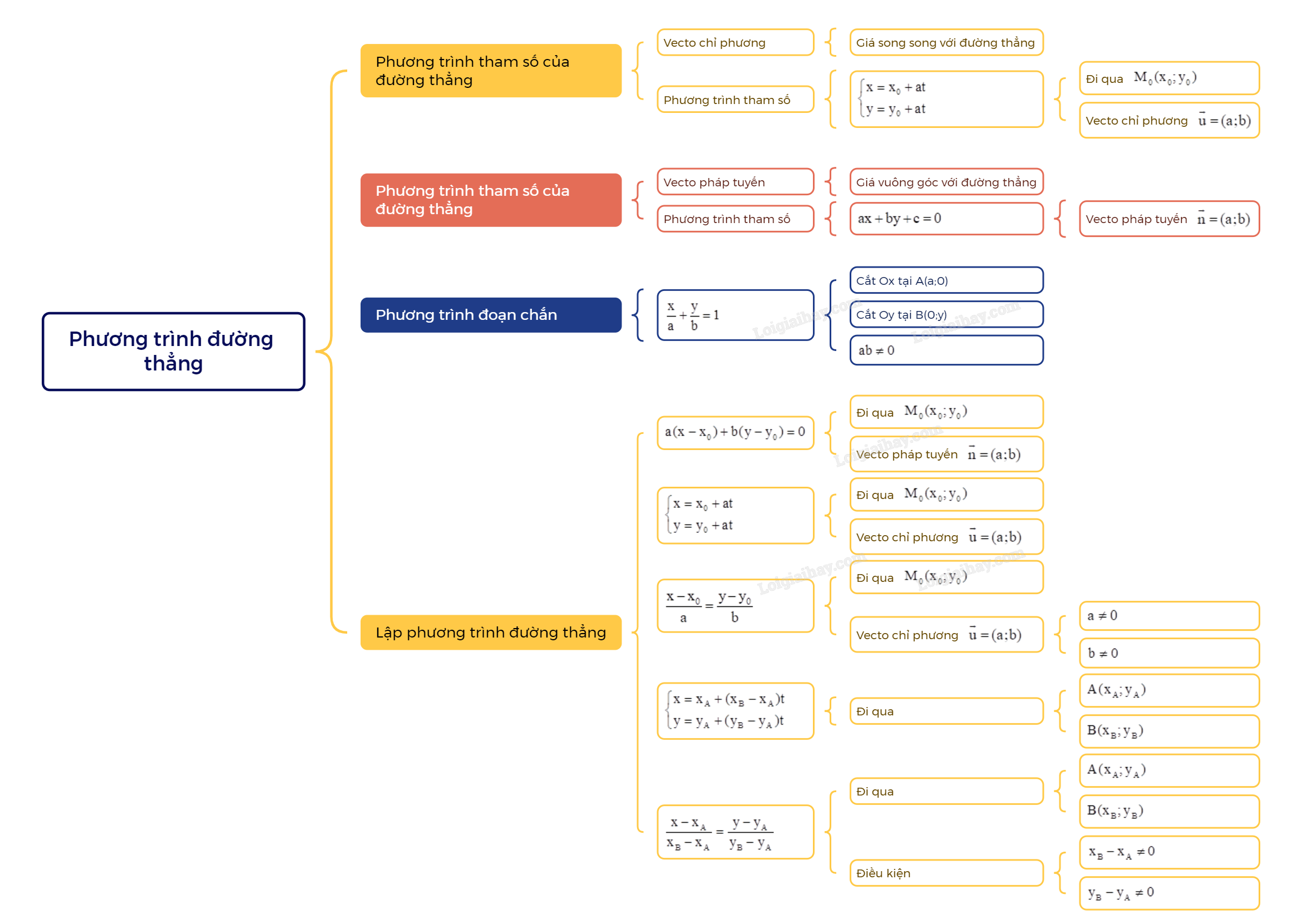}} \Leftrightarrow \frac{{x + 3}}{4} = \frac{{y - 4}}{{ - 5}} \Leftrightarrow 5x + 4y - 1 = 0\).