Lý thuyết Phép nhân đa thức SGK Toán 8 - Kết nối tri thức1. Nhân đơn thức với đa thức Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên 1. Nhân đơn thức với đa thức + Nhân hai đơn thức như thế nào? Muốn nhân hai đơn thức, ta nhân hai hệ số với nhau và nhân hai phần biến với nhau. Ví dụ: (−3x2y)(4xy)=[(−3.4)].(x2.x).(y.y)=−12.x3.y2 + Nhân đơn thức với đa thức như thế nào? Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau. Ví dụ: 3x2y(2x2y−xy+3y2)=(3x2y).(2x2y)−(3x2y).(xy)+(3x2y).(3y2)=3.2.(x2.x2)(y.y)−3.(x2.x).(y.y)+3.3.x2.(y.y2)=6x4y2−3x3.y2+9x2y3 2. Nhân đa thức với đa thức + Nhân hai đa thức như thế nào? Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau. Phép nhân đa thức cũng có các tính chất tương tự phép nhân các số. + Giao hoán: A.B = B.A + Kết hợp: (A.B).C = A.(B.C) + Phân phối của phép nhân đối với phép cộng: (A + B).C = AB + AC Ví dụ: (xy+1)(xy−3)=(xy).(xy)+xy−3xy−3=x2y2−2xy−3 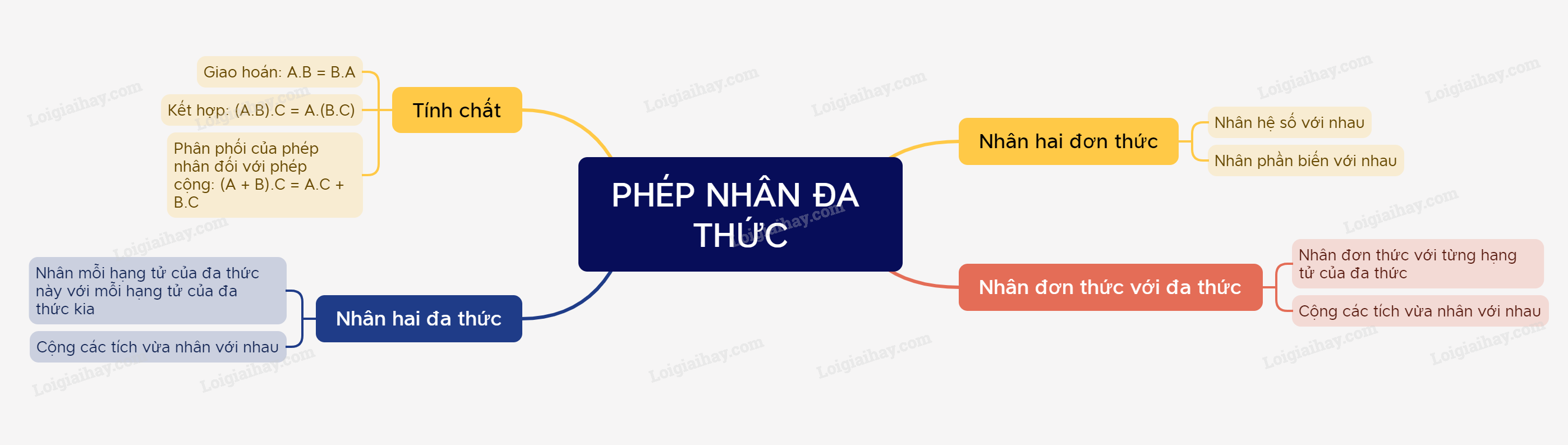
|













