Lý thuyết Một số hệ thức về cạnh và góc trong tam giác vuông Toán 9 Cánh diều1. Tính cạnh góc vuông theo cạnh huyền và tỉ số lượng giác của góc nhọn Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề. Cạnh góc vuông = (cạnh huyền ) × (sin góc đối) = (cạnh huyền ) × (cosin góc kề) 1. Tính cạnh góc vuông theo cạnh huyền và tỉ số lượng giác của góc nhọn
Ví dụ 1:
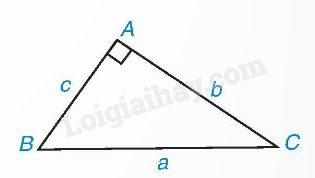
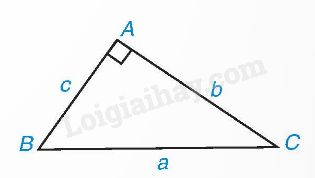
Trong tam giác ABC vuông tại A, ta có: \(\begin{array}{l}b = a.\sin B = a.\cos C;\\c = a.\sin C = a.\cos B.\end{array}\) 2. Tính cạnh góc vuông theo cạnh góc vuông còn lại và tỉ số lượng giác của góc nhọn
Ví dụ 2:
Trong tam giác ABC vuông tại A, ta có: \(\begin{array}{l}b = c.\tan B = c.\cot C;\\c = b.\tan C = b.\cot B.\end{array}\) 3. Áp dụng tỉ số lượng giác của góc nhọn để giải tam giác vuông Giải tam giác vuông là tìm tất cả độ dài các cạnh và số đo các góc còn lại của tam giác đó.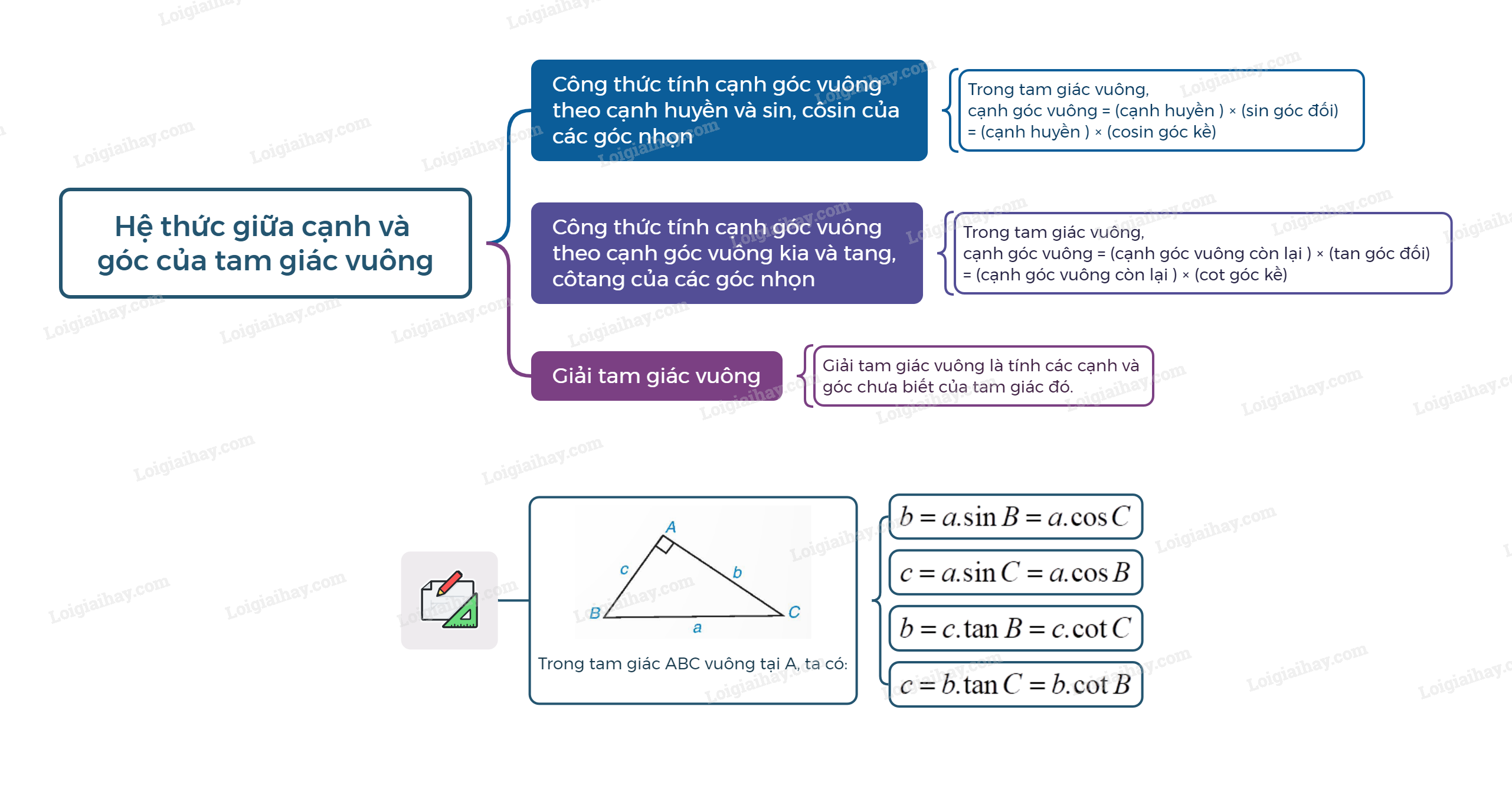
 Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
