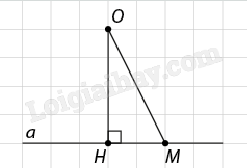
Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá

A. Lý thuyết

1. Khoảng cách từ một điểm đến một đường thẳng

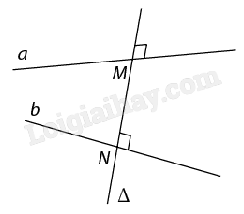
Lưu ý:

- d(O,a) là nhỏ nhất so với khoảng cách từ O đến mọi điểm thuộc a.

- d(O,a) = 0 khi và chỉ khi O thuộc a.

2. Khoảng cách giữa hai đường thẳng song song, giữa đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song

a) Khoảng cách giữa hai đường thẳng song song

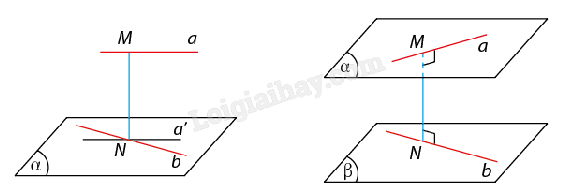
b) Khoảng cách giữa đường thẳng và mặt phẳng song song

c) Khoảng cách giữa hai mặt phẳng song song

Lưu ý: \(d((\alpha ),(\beta )) = d(M,(\beta ))\) với \(M \in (\alpha )\) và \(d((\alpha ),(\beta )) = d(M',(\alpha ))\), với \(M' \in (\beta )\).

3. Đường vuông góc chung và khoảng cách giữa hai đường thẳng chéo nhau

a) Khái niệm

b) Tính chất

Lưu ý: Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách nhỏ nhất trong các khoảng cách giữa hai điểm bất kì lần lượt nằm trên hai đường thẳng đó.

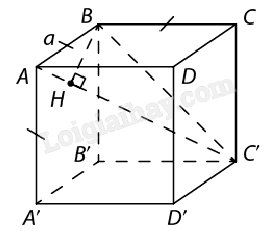
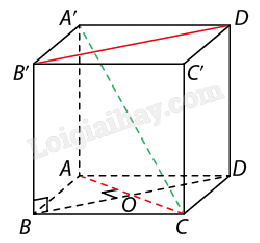
B. Bài tập

Bài 1: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính khoảng cách từ điểm B đến đường chéo AC’.

Giải:

Khoảng cách từ B đến AC’ là chiều cao BH của tam giác BAC’.

Ta có:

 ABCD.A’B’C’D’ là hình lập phương nên \(AB \bot (BB'C'C) \Rightarrow AB \bot BC'\); hay tam giác ABC’ vuông tại B.

AB = a, \(BC' = \sqrt 2 a\) (BB’C’C là hình vuông cạnh a) nên \(AC' = \sqrt 3 a\) (đường chéo hình lập phương cạnh a).

\(BA.BC' = BH.AC = 2{S_{\Delta ABC}}\). Suy ra \(BH = \frac{{\sqrt 6 }}{3}a\).

Vậy \(d(B;AC') = BH = \frac{{\sqrt 6 }}{3}a\).

Bài 2: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng các từ S đến mặt phẳng (ABCD).

Giải:

Hai mặt phẳng (SAB) và (ABCD) vuông góc nhau theo giao tuyến AB.

Gọi H là trung điểm của AB thì \(SH \bot AB\). Suy ra \(SH \bot (ABCD)\) tại H.

Vậy \(d(S,ABCD) = SH = \frac{{\sqrt 3 }}{2}a\) (chiều cao của tam giác đều cạnh a).

Bài 3: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính khoảng cách giữa hai đường thẳng BC’ và AD’.

Giải:

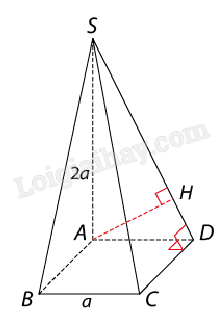
Do ABCD.A’B’C’D’ là hình lập phương nên ABC’D’ là hình chữ nhật.

Do đó BC’ // AD’.

Vậy \(d(BC',AD') = d(A,BC') = AB = a\).

Bài 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Biết \(SA \bot (ABCD)\) và SA = 2a. Tính khoảng cách giữa đường thẳng AB và mặt phẳng (SCD).

Giải:

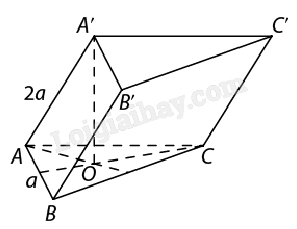
AB // CD, \(CD \subset (SCD)\) nên AB // (SCD).

Vậy \(d(AB,(SCD)) = d(A,(SCD))\).

Ta có \(CD \bot SA\) và \(CD \bot AD\) nên \(CD \bot (SAD)\). Vậy \((SAD) \bot (SCD)\).

Mà \((SAD) \cap (SCD) = SD\) nên gọi H là hình chiếu của A trên SD thì \(AH \bot (SCD)\) và \(d(A,(SCD)) = AH\).

Xét tam giác SAD vuông tại A có SA = 2a, AD = a nên \(S{D^2} = A{D^2} + S{A^2} = 5{a^2}\) hay \(SD = \sqrt 5 a\).

Suy ra \(AH.SD = SA.AD \Rightarrow AH = \frac{{SA.AD}}{{SD}} = \frac{{2\sqrt 5 }}{5}a\).

Vậy \(d(AB,(SCD)) = \frac{{2\sqrt 5 }}{5}a\).

Bài 5: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, A’ cách đều A, B, C và AA’ = 2a. Tính khoảng cách giữa hai đáy của hình lăng trụ này.

Giải:

Do (ABC) // (A’B’C’) nên \(d((ABC),(A'B'C')) = d(A',(ABC))\).

Vì tam giác ABC đều và AA’ = A’B = A’C nên A’.ABC là hình chóp tam giác đều.

Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Ta có: A’.ABC là hình chóp đều nên A’O vuông góc với (ABC) tại O. Vậy d(A’,(ABC)) = A’O.

Ta có \(A'O = \sqrt {A'{A^2} - A{O^2}}  = \frac{{\sqrt {33} }}{3}a\).

Vậy \(d((ABC),(A'B'C')) = \frac{{\sqrt {33} }}{3}a\).

Bài 6: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính khoảng cách giữa các cặp đường thẳng sau:

a) BB’ và AC.

b) BB’ và A’C.

c) AC và B’D’.

Giải:

a) Gọi O là tâm hình vuông ABCD. Ta có:

\(BO \bot AC\) (ABCD là hình vuông).

\(BO \bot BB'\) (do ABCD.A’B’C’D’ là hình lập phương nên \(BB' \bot (ABCD)\)); BO cắt AC, BB’ lần lượt tại O, B.

Suy ra BO là đoạn vuông góc chung của hai đường thẳng BB’ và AC.

Mà ABCD là hình vuông cạnh a, nên \(BO = \frac{{\sqrt 2 }}{2}a\).

Vậy khoảng cách giữa hai đường thẳng chéo nhau BB’ và AC là \(BO = \frac{{\sqrt 2 }}{2}a\).

b) Ta có: BB’ // AA’, suy ra (ACA’) chứa AC và song song với BB’.

Suy ra \(d(BB';AC) = d(BB';(ACA')) = d(B;(ACA')) = BO = \frac{{\sqrt 2 }}{2}a\).

c) Ta có AC và B’D’ lần lượt nằm trên hai mặt phẳng song song nhau là (ABCD) và (A’B’C’D’) nên \(d(AC,B'D') = d((ABCD),(A'B'C'D')) = AA' = a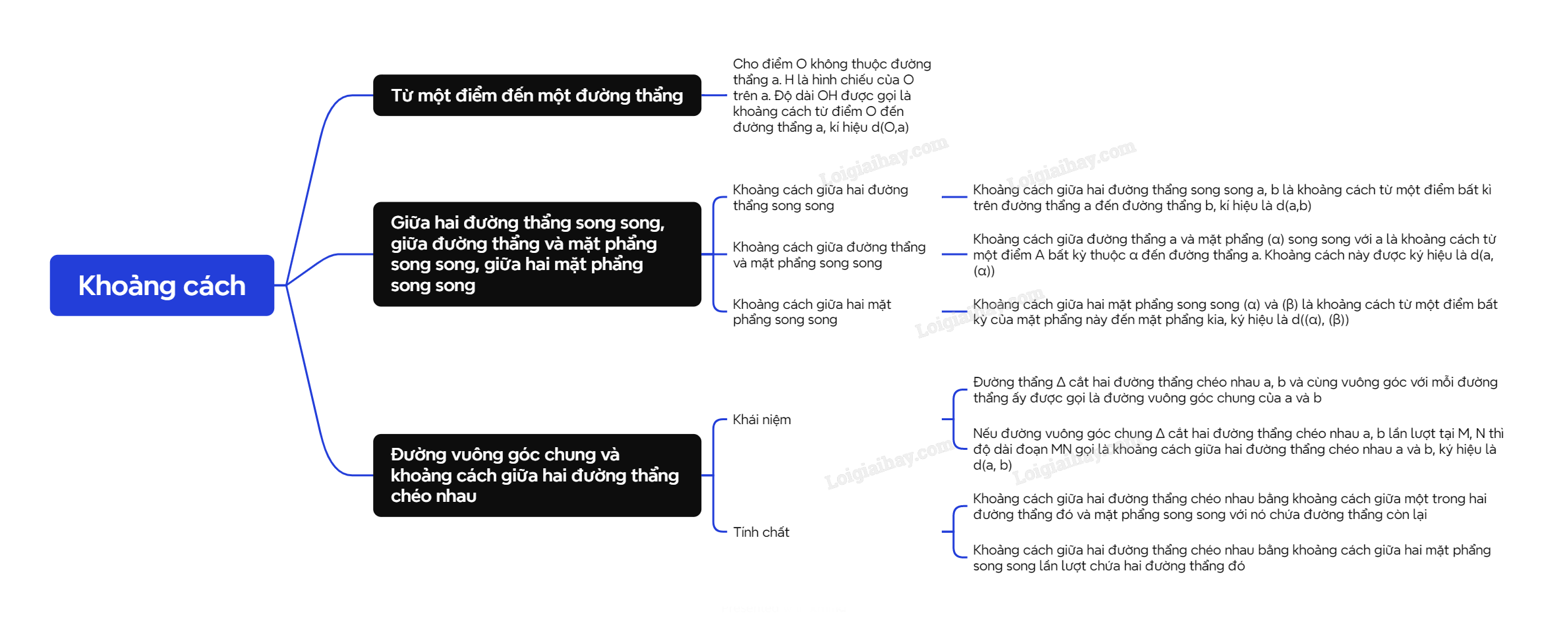\).