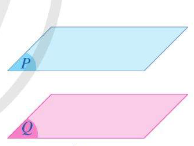
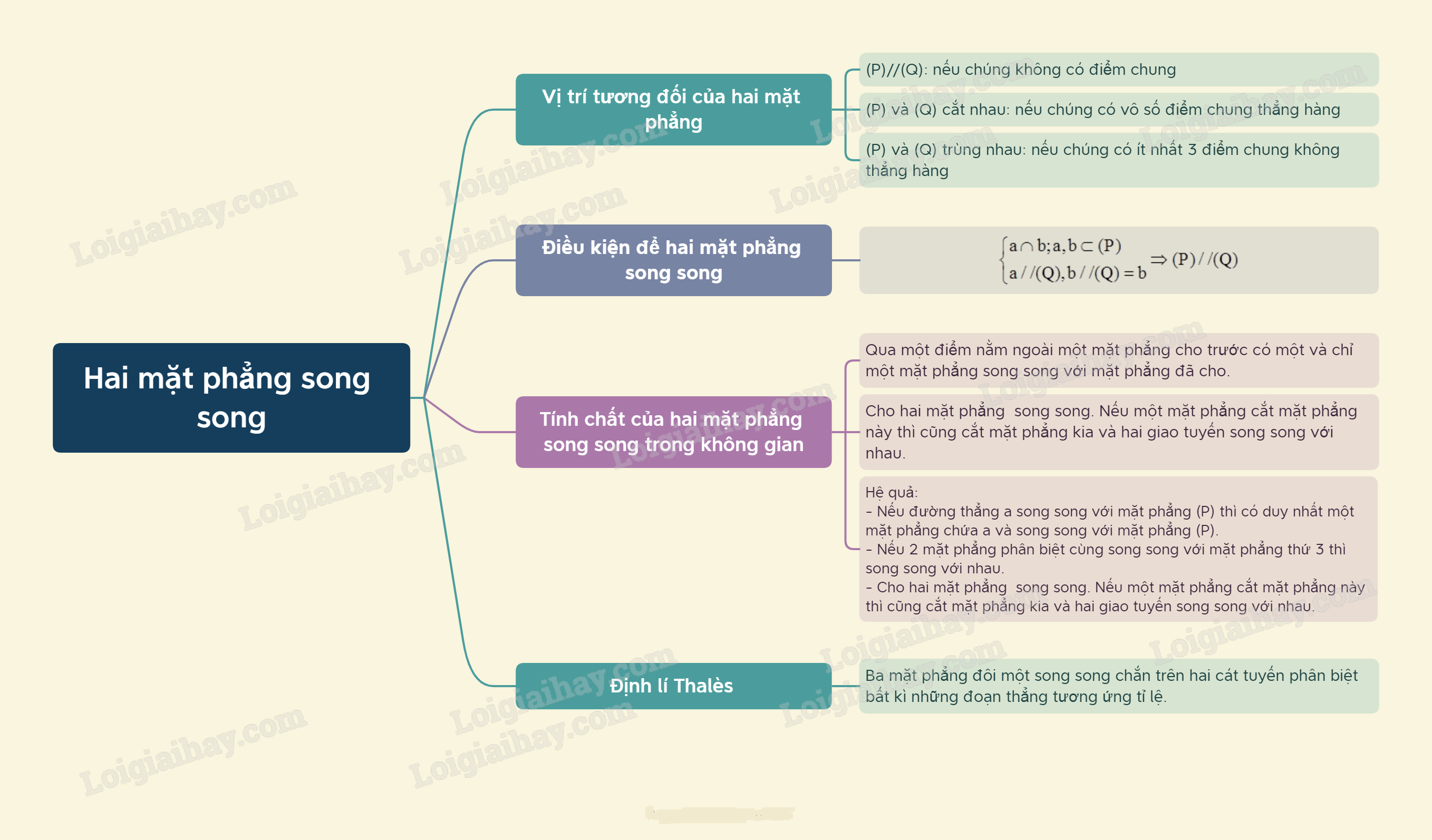
Lý thuyết Hai mặt phẳng song song - SGK Toán 11 Cánh Diều

I. Hai mặt phẳng song song

Hai mặt $\left( P \right)$ và $\left( Q \right)$ được gọi là song song với nhau nếu chúng không có điểm chung. Kí hiệu$\left( P \right)$// $\left( Q \right)$ hay $\left( Q \right)$//$\left( P \right)$.

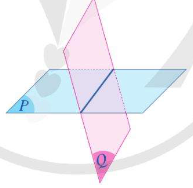
*Nhận xét: Hai mặt $\left( P \right)$ và $\left( Q \right)$ có diểm chung. Khi đó, chúng cắt nhau theo một đường thẳng.

II. Điều kiện và tính chất

• Nếu mặt phẳng $\left( P \right)$ chứa hai đường thẳng cắt nhau a,b  và a,b cùng song song với mặt phẳng phẳng $\left( Q \right)$thì $\left( P \right)$song song với $\left( Q \right)$

• Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.

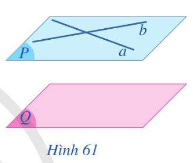
* Hệ quả:

- Nếu đường thẳng a song song với mặt phẳng $\left( Q \right)$ thì có duy nhất một mặt phẳng chứa a và song song với mặt phẳng $\left( Q \right)$

- Nếu 2 mặt phẳng phân biệt cùng song song với mặt phẳng thứ 3 thì song song với nhau.

• Cho hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ song song. Nếu mặt phẳng $\left( R \right)$ cắt mặt phẳng $\left( P \right)$thì cũng cắt mặt phẳng $\left( Q \right)$và hai giao tuyến song song với nhau.

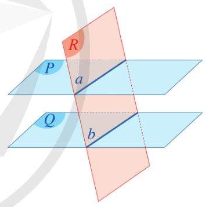
III. Định lí Thalès

Nếu a, b là hai cát tuyến bất kì cắt 3 mặt phẳng song song $\left( P \right)$ , $\left( Q \right)$và$\left( R \right)$ lần lượt tại các điểm A, B, C và A’, B’, C’ thì

$\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}$