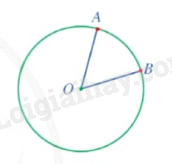
Lý thuyết Góc ở tâm, góc nội tiếp Toán 9 Cánh diều1. Góc ở tâm Định nghĩa Góc ở tâm là góc có đỉnh trùng với tâm đường tròn. Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh 1. Góc ở tâm Định nghĩa
Nhận xét: Đường kính chia đường tròn thành hai phần, mỗi phần được gọi là một nửa đường tròn. 2. Cung, số đo cung Cung Phần đường tròn nối liền hai điểm A, B trên đường tròn được gọi là một cung (hay cung tròn) AB, kí hiệu là $\overset\frown{AB}$.
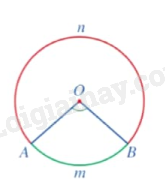
Góc ở tâm \(\widehat {AOB}\) chắn cung AnB hay cung AnB bị chắn bởi góc ở tâm \(\widehat {AOB}\). $\overset\frown{AnB}$ là cung nhỏ và $\overset\frown{AmB}$ là cung lớn. Số đo cung
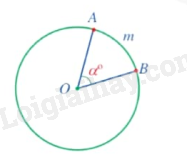
Quy ước: Khi hai mút của cung trùng nhau, ta có “cung không” với số đo \({0^0}\) và cung cả đường tròn có số đo \({360^0}\). Nhận xét: Góc ở tâm chắn một cung mà cung đó là nửa đường tròn thì có số đo bằng \({180^0}\). Nếu điểm C là một điểm nằm trên cung AB thì sđ$\overset\frown{ACB}$ = sđ$\overset\frown{AC}$ + sđ$\overset\frown{CB}$. Chú ý: - Khác với so sánh hai góc, ta chỉ so sánh hai cung trong một đường tròn hay trong hai đường tròn bằng nhau. Cụ thể: + Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau; + Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn. Hai cung AB và CD bằng nhau được kí hiệu là $\overset\frown{AB}=\overset\frown{CD}$. Cung EG nhỏ hơn cung HK được kí hiệu là $\overset\frown{EG}<\overset\frown{HK}$. Trong trường hợp này, ta cũng nói cung HK lớn hơn cung EG và kí hiệu là $\overset\frown{HK}>\overset\frown{EG}$. - Cho điểm \(A\) thuộc đường tròn \((O)\) và số thực \(\alpha \) với \(0 < \alpha < 360\). Sử dụng thược thẳng và thước đo độ, ta vẽ điểm \(B\) thuộc đường tròn \((O)\) như sau: + Nếu \(0 < \alpha \le 180\) thì ta vẽ theo chiểu quay của kim đồng hồ góc ở tâm AOB có số đo bằng \({\alpha ^0}\). Khi đó sđ$\overset\frown{AmB}={{\alpha }^{0}}$
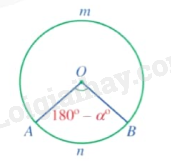
+ Nếu \(180 < \alpha \le 360\) thì ta vẽ theo ngược chiểu quay của kim đồng hồ góc ở tâm AOB có số đo bằng \({\alpha ^0} - {180^0}\). Khi đó sđ$\overset\frown{AnB}={{\alpha }^{0}}$.
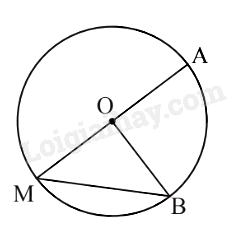
3. Góc nội tiếp Định nghĩa
Định lí
Số đo góc nội tiếp
Ví dụ:
\(\widehat {AMB}\) là góc nội tiếp chắn $\overset\frown{AB}$ trên đường tròn (O) nên $\widehat{AMB}=\frac{1}{2}$sđ$\overset\frown{AB}$. Nhận xét: Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau. 
|