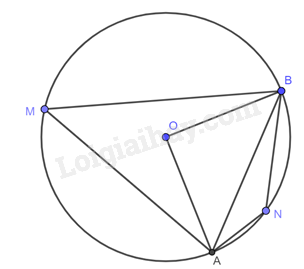
Giải bài tập 2 trang 117 SGK Toán 9 tập 1 - Cánh diềuCho đường tròn (left( {O;R} right)) và dây (AB) sao cho (widehat {AOB} = 90^circ ). Giả sử (M,N) lần lượt là các điểm thuộc cung lớn (AB) và cung nhỏ (AB) ((M,N) khác (A) và (B)). a) Tính độ dài đoạn thẳng (AB) theo (R). b) Tính số đo các góc (ANB) và (AMB). Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Cho đường tròn (O;R)(O;R) và dây ABAB sao cho ^AOB=90∘ˆAOB=90∘. Giả sử M,NM,N lần lượt là các điểm thuộc cung lớn ABAB và cung nhỏ ABAB (M,NM,N khác AA và BB). a) Tính độ dài đoạn thẳng ABAB theo RR. b) Tính số đo các góc ANBANB và AMBAMB. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Dựa vào tính chất góc ở tâm và góc nội tiếp để tính. Lời giải chi tiết
OA2+OB2=AB2⇒AB2=R2+R2=2R2⇒AB=R√2OA2+OB2=AB2⇒AB2=R2+R2=2R2⇒AB=R√2 b) Xét đường tròn (O)(O): +) Vì M thuộc cung lớn AB nên ^AMBˆAMB là góc nội tiếp và ^AOBˆAOB là góc ở tâm cùng chắn cung nhỏ ABAB nên: ^AMB=12^AOB=12.90∘=45∘ˆAMB=12ˆAOB=12.90∘=45∘. +) Số đo cung lớn AB là: sđ⌢ABlớn=360∘−sđ⌢ABnhỏ=360∘−90∘=270∘ +) Vì N thuộc cung nhỏ AB nên ^ANB là góc nội tiếp chắn cung lớn AB nên: ^ANB=12sđ⌢ABlớn=12.270∘=135∘. Vậy ^AMB=45∘,^ANB=135∘.
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|