Lý thuyết Giới hạn của hàm số - SGK Toán 11 Cùng khám phá

I. Giới hạn của hàm số tại một điểm

I. Giới hạn của hàm số tại một điểm

1. Giới hạn hữu hạn của hàm số tại một điểm

Cho điểm \({x_0}\) thuộc khoảng K và hàm số \(y = f(x)\) xác định trên K hoặc trên \(K\backslash \left\{ {{x_0}} \right\}\). Ta nói hàm số \(y = f(x)\) có giới hạn hữu hạn là số L khi \(x\) dần tới \({x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} \in K\backslash \left\{ {{x_0}} \right\}\) và \({x_n} \to {x_0}\), ta có\(f({x_n}) \to L\)

Kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) hay \(f(x) \to L\), khi \({x_n} \to {x_0}\).

2. Định lí về giới hạn hữu hạn của hàm số

a, Cho \(y = f(x)\) và \(y = g(x)\) là các hàm số xác định trên \(K\backslash \left\{ {{x_0}} \right\}\)

Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) và \(\mathop {\lim }\limits_{x \to {x_0}} g(x) = M\), trong đó M, L là các số thực thì:

\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x) \pm g(x)} \right] = L \pm M\)

\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x).g(x)} \right] = L.M\)

\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {\frac{{f(x)}}{{g(x)}}} \right] = \frac{L}{M}\left( {M \ne 0} \right)\)

b, Nếu \(f(x) \ge 0\)với mọi \(x \in \left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}\) và \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) thì \(L \ge 0\) và \(\mathop {\lim }\limits_{x \to {x_0}} \sqrt {f(x)} = \sqrt L \).

3. Giới hạn vô cực

Cho điểm \({x_0}\)thuộc khoảng K và hàm số \(y = f(x)\) xác định trên K hoặc \(K\backslash \left\{ {{x_0}} \right\}\). Ta nói hàm số \(f(x)\) có giới hạn là \( + \infty \)(hoặc \( - \infty \) ) khi \(x\) dần tới \({x_0}\) nếu với mọi dãy số \(\left( {{x_n}} \right)\), \({x_n} \in K\backslash \left\{ {{x_0}} \right\}\) mà \(\lim {x_n} = {x_0}\), ta đều có \(\lim f\left( {{x_n}} \right) = + \infty \) (hoặc \(\lim f\left( {{x_n}} \right) = - \infty \) kí hiệu kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = + \infty \) hoặc \(f(x) \to + \infty \) khi \(x \to {x_0}\) (tương tự kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = - \infty \) hoặc \(f(x) \to - \infty \) khi \(x \to {x_0}\) ).

II. Giới hạn một phía

Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {{x_0};b} \right)\).

Ta nói \(y = f(x)\) có giới hạn bên phải là số L khi \(x \to {x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì,\({x_0} < {x_n} < b\) và \({x_n} \to {x_0}\)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L\).

Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a;{x_0}} \right)\).

Ta nói \(y = f(x)\) có giới hạn bên phải là số L khi \(x \to {x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì,\(a < {x_n} < {x_0}\) và \({x_n} \to {x_0}\)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = L\).

*Định lí:

\(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = \mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L\)

III. Giới hạn của hàm số tại vô cực

1. Giới hạn hữu hạn của hàm số tại vô cực

Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a; + \infty } \right)\). Ta nói hàm số \(f(x)\) có giới hạn là số L khi \(x \to + \infty \) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì \({x_n} > a\) và \({x_n} \to + \infty \)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = L\) hay \(f(x) \to L\) khi \(x \to + \infty \).

Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( { - \infty ;a} \right)\). Ta nói hàm số \(f(x)\) có giới hạn là số L khi \(x \to - \infty \) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì \({x_n} < a\) và \({x_n} \to - \infty \)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = L\) hay \(f(x) \to L\) khi \(x \to - \infty \).

* Nhận xét:

Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.
Với c là hằng số, k là một số nguyên dương ta có:

\(\mathop {\lim }\limits_{x \to \pm \infty } c = c,\)\(\mathop {\lim }\limits_{x \to \pm \infty } (\frac{c}{{{x^k}}}) = 0\)

2. Giới hạn vô cực của hàm số tại vô cực

a, Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a; + \infty } \right)\).

Ta nói hàm số \(f(x)\) có giới hạn là \( + \infty \) khi \(x \to + \infty \) nếu với dãy số \(\left( {{x_n}} \right),{x_n} > a\)và \(\lim {x_n} = + \infty \), ta đều có \(\lim f\left( {{x_n}} \right) = + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \) hoặc \(f(x) \to + \infty \) khi \(x \to + \infty \) .

b, Cho hàm số \(y = f(x)\)xác định trên khoảng \(\left( { - \infty ;a} \right)\).

Ta nói hàm số \(f(x)\)có giới hạn là \( + \infty \) khi \(x \to - \infty \) nếu với dãy số \(\left( {{x_n}} \right),{x_n} < a\)và \(\lim {x_n} = - \infty \), ta đều có \(\lim f\left( {{x_n}} \right) = + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = + \infty \) hoặc \(f(x) \to + \infty \) khi \(x \to - \infty \)

Từ hai định nghĩa trên, ta có định nghĩa \(f(x) \to - \infty \) khi \(x \to + \infty \) (hay \(x \to - \infty \)) như sau:

c, \(\mathop {\lim }\limits_{x \to + \infty } f(x) = - \infty \Leftrightarrow \mathop {\lim }\limits_{x \to + \infty } \left[ { - f(x)} \right] = + \infty \)

d, \(\mathop {\lim }\limits_{x \to - \infty } f(x) = - \infty \Leftrightarrow \mathop {\lim }\limits_{x \to - \infty } \left[ { - f(x)} \right] = + \infty \)

* Chú ý:

\(\mathop {\lim }\limits_{x \to + \infty } {x^k} = + \infty ,k \in {\mathbb{Z}^ + }.\)
\(\mathop {\lim }\limits_{x \to - \infty } {x^k} = + \infty ,\) k là số nguyên dương chẵn.
\(\mathop {\lim }\limits_{x \to - \infty } {x^k} = - \infty ,\) k là số nguyên dương lẻ.

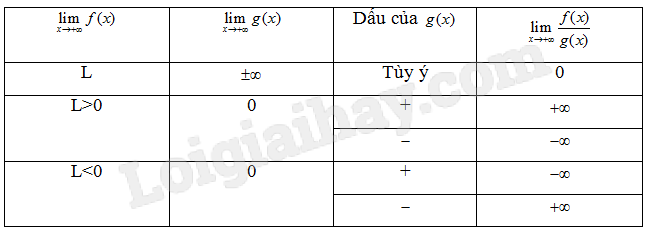
3. Quy tắc tìm giới hạn của tích và thương tại vô cực

*Giới hạn của tích\(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x).g(x)} \right]\)