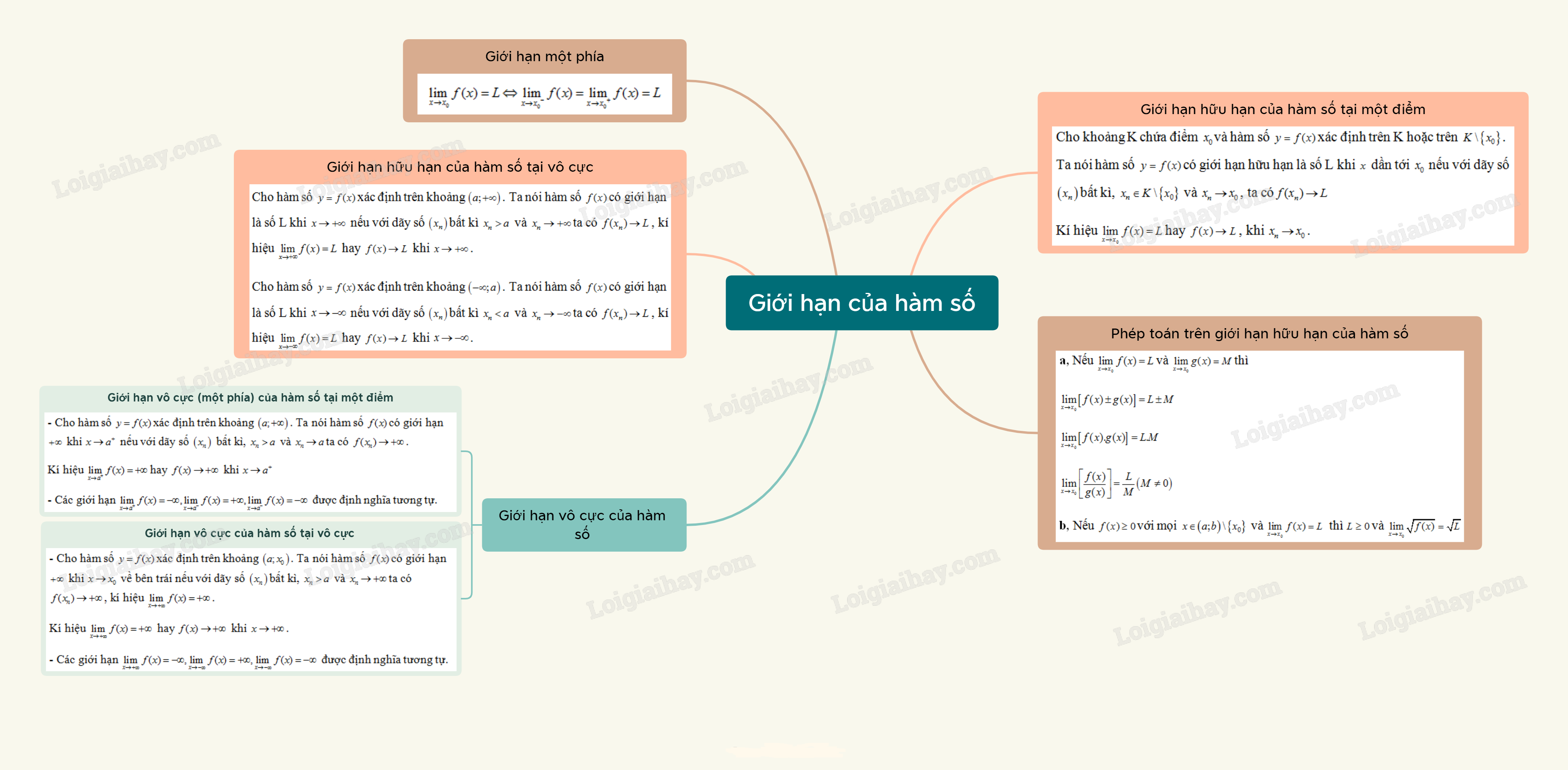
Lý thuyết Giới hạn của hàm số - SGK Toán 11 Cánh Diều

I. Giới hạn hữu hạn của hàm số tại một điểm

1. Định nghĩa

Cho khoảng K chứa điểm ${x_0}$và hàm số $f(x)$ xác định trên K hoặc trên $K\backslash \left\{ {{x_0}} \right\}$. Hàm số $f(x)$có giới hạn là số L khi $x$ dần tới ${x_0}$ nếu với dãy số $\left( {{x_n}} \right)$bất kì, ${x_n} \in K\backslash \left\{ {{x_0}} \right\}$ và ${x_n} \to {x_0}$, ta có$f({x_n}) \to L$

Kí hiệu $\mathop {\lim }\limits_{x \to {x_0}} f(x) = L$ hay $f(x) \to L$, khi ${x_n} \to {x_0}$.

2. Phép toán trên giới hạn hữu hạn của hàm số

a, Nếu $\mathop {\lim }\limits_{x \to {x_0}} f(x) = L$ và $\mathop {\lim }\limits_{x \to {x_0}} g(x) = M$$\left( {L,M \in \mathbb{R}} \right)$thì

$\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x) \pm g(x)} \right] = L \pm M$

$\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x).g(x)} \right] = L.M$

$\mathop {\lim }\limits_{x \to {x_0}} \left[ {\frac{{f(x)}}{{g(x)}}} \right] = \frac{L}{M}\left( {M \ne 0} \right)$

b, Nếu $f(x) \ge 0$ với mọi $x \in \left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}$ và $\mathop {\lim }\limits_{x \to {x_0}} f(x) = L$ thì $L \ge 0$ và $\mathop {\lim }\limits_{x \to {x_0}} \sqrt {f(x)}  = \sqrt L$.

3. Giới hạn một phía

- Cho hàm số $y = f(x)$ xác định trên khoảng $\left( {a;{x_0}} \right)$. Số L được gọi là giới hạn bên trái của hàm số $y = f(x)$ khi $x \to {x_0}$ nếu với dãy số $\left( {{x_n}} \right)$ bất kì thỏa mãn $a < {x_n} < {x_0}$ và ${x_n} \to {x_0}$ ta có $f({x_n}) \to L$, kí hiệu $\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = L$.

- Cho hàm số $y = f(x)$ xác định trên khoảng $\left( {{x_0};b} \right)$. Số L là giới hạn bên của hàm số $y = f(x)$ khi $x \to {x_0}$ nếu với dãy số $\left( {{x_n}} \right)$bất kì thỏa mãn ${x_0} < {x_n} < b$ và ${x_n} \to {x_0}$ ta có $f({x_n}) \to L$, kí hiệu $\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L$.

*Nhận xét: $\mathop {\lim }\limits_{x \to {x_0}} f(x) = L \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = \mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L$

II. Giới hạn hữu hạn của hàm số tại vô cực

- Cho hàm số $y = f(x)$xác định trên khoảng $\left( {a; + \infty } \right)$. Ta nói hàm số $f(x)$ có giới hạn là số L khi $x \to  + \infty$ nếu với dãy số $\left( {{x_n}} \right)$bất kì ${x_n} > a$ và ${x_n} \to  + \infty$ta có $f({x_n}) \to L$, kí hiệu $\mathop {\lim }\limits_{x \to  + \infty } f(x) = L$ hay $f(x) \to L$ khi $x \to  + \infty$.

- Cho hàm số $y = f(x)$ xác định trên khoảng $\left( { - \infty ;b} \right)$. Ta nói hàm số $f(x)$ có giới hạn là số L khi $x \to  - \infty$ nếu với dãy số $\left( {{x_n}} \right)$bất kì ${x_n} < b$ và ${x_n} \to  - \infty$ta có $f({x_n}) \to L$, kí hiệu $\mathop {\lim }\limits_{x \to  - \infty } f(x) = L$ hay $f(x) \to L$ khi $x \to  - \infty$.

* Nhận xét:

- Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.

- Với c là hằng số, k là một số nguyên dương ta có:

$\mathop {\lim }\limits_{x \to  + \infty } c = c$, $\mathop {\lim }\limits_{x \to  - \infty } c = c$,$\mathop {\lim }\limits_{x \to  + \infty } (\frac{c}{{{x^k}}}) = 0,\mathop {\lim }\limits_{x \to  - \infty } (\frac{c}{{{x^k}}}) = 0$.

III. Giới hạn vô cực (một phía) của hàm số tại một điểm

- Cho hàm số $y = f(x)$xác định trên khoảng $\left( {a; + \infty } \right)$. Ta nói hàm số $f(x)$có giới hạn $+ \infty$ khi $x \to {a^ + }$ nếu với dãy số $\left( {{x_n}} \right)$ bất kì, ${x_n} > a$ và ${x_n} \to a$ta có $f({x_n}) \to  + \infty$.

Kí hiệu $\mathop {\lim }\limits_{x \to {a^ + }} f(x) =  + \infty$hay $f(x) \to  + \infty$ khi $x \to {a^ + }$

- Các giới hạn $\mathop {\lim }\limits_{x \to {a^ + }} f(x) =  - \infty ,\mathop {\lim }\limits_{x \to {a^ - }} f(x) =  + \infty ,\mathop {\lim }\limits_{x \to {a^ - }} f(x) =  - \infty$ được định nghĩa tương tự.

IV. Giới hạn vô cực của hàm số tại vô cực

- Cho hàm số $y = f(x)$ xác định trên khoảng $\left( {a;{x_0}} \right)$. Ta nói hàm số $f(x)$có giới hạn $+ \infty$ khi $x \to {x_0}$ về bên trái nếu với dãy số $\left( {{x_n}} \right)$bất kì, ${x_n} > a$ và ${x_n} \to  + \infty$ ta có $f({x_n}) \to  + \infty$, kí hiệu $\mathop {\lim }\limits_{x \to  + \infty } f(x) =  + \infty$.

Kí hiệu $\mathop {\lim }\limits_{x \to  + \infty } f(x) =  + \infty$ hay $f(x) \to  + \infty$ khi $x \to  + \infty$.

- Các giới hạn $\mathop {\lim }\limits_{x \to  + \infty } f(x) =  - \infty ,\mathop {\lim }\limits_{x \to  - \infty } f(x) =  + \infty ,\mathop {\lim }\limits_{x \to  - \infty } f(x) =  - \infty$ được định nghĩa tương tự.

* Chú ý:

• $\mathop {\lim }\limits_{x \to  + \infty } {x^k} =  + \infty ,k \in {\mathbb{Z}^ + }.$
• $\mathop {\lim }\limits_{x \to  - \infty } {x^k} =  + \infty ,$ k là số nguyên dương chẵn.
• $\mathop {\lim }\limits_{x \to  - \infty } {x^k} =  - \infty ,$ k là số nguyên dương lẻ.
•