Giải mục 1 trang 66, 67, 68, 69 SGK Toán 11 tập 1 - Cánh Diều

Hoạt động 1

Xét hàm số $f\left( x \right) = 2x.$

a) Xét dãy số $\left( {{x_n}} \right),$ với ${x_n} = 1 + \frac{1}{n}.$ Hoàn thành bảng giá trị $f\left( {{x_n}} \right)$ tương ứng.

Các giá trị tương ứng của hàm số $f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right),...$ lập thành một dãy số mà ta kí hiệu là $\left( {f\left( {{x_n}} \right)} \right).$ Tìm $\lim f\left( {{x_n}} \right).$

b) Chứng minh rằng với dãy số bất kì $\left( {{x_n}} \right),{x_n} \to 1$ ta luôn có $f\left( {{x_n}} \right) \to 2.$

Phương pháp giải:

Sử dụng định lí về giới hạn hữu hạn kết hợp với một số giới hạn cơ bản.

Nếu $\mathop {\lim }\limits_{n \to  + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to  + \infty } {v_n} = b$ thì

$\mathop {\lim }\limits_{n \to  + \infty } ({u_n} \pm {v_n}) = a \pm b$

$\mathop {\lim }\limits_{n \to  + \infty } ({u_n}.{v_n}) = a.b$

$\mathop {\lim }\limits_{n \to  + \infty } (\frac{{{u_n}}}{{{v_n}}}) = \frac{a}{b}\left( {b \ne 0} \right)$

Lời giải chi tiết:

a,

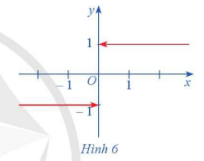
$\lim f\left( {{x_n}} \right) = \lim \left( {2.\frac{{n + 1}}{n}} \right) = \lim 2.\lim \left( {1 + \frac{1}{n}} \right) = 2.\left( {1 + 0} \right) = 2$

b) Lấy dãy số bất kì $\left( {{x_n}} \right),{x_n} \to 1$ ta có $f\left( {{x_n}} \right) = 2{x_n}.$

 $\lim f\left( {{x_n}} \right) = \lim \left( {2{x_n}} \right) = \lim 2.\lim {x_n} = 2.1 = 2$

Quảng cáo

Luyện tập, vận dụng 1

Sử dụng định nghĩa, chứng minh rằng $\mathop {\lim }\limits_{x \to 2} {x^2} = 4.$

Phương pháp giải:

Sử dụng định nghĩa giới hạn hữu hạn của hàm số tại một điểm

Cho khoảng K chứa điểm ${x_0}$và hàm số $f(x)$xác định trên K hoặc trên $K\backslash \left\{ {{x_0}} \right\}$. Hàm số $f(x)$có giới hạn là số L khi $x$ dần tới ${x_0}$ nếu với dãy số $\left( {{x_n}} \right)$bất kì, ${x_n} \in K\backslash \left\{ {{x_0}} \right\}$ và ${x_n} \to {x_0}$, ta có$f({x_n}) \to L$

Lời giải chi tiết:

Giả sử $\left( {{x_n}} \right)$ là dãy số bất kì thỏa mãn $\lim {x_n} = 2.$

Ta có $\lim x_n^2 = {2^2} = 4$

Vậy $\mathop {\lim }\limits_{x \to 2} {x^2} = 4.$

Hoạt động 2

Cho hai hàm số $f\left( x \right) = {x^2} - 1,g\left( x \right) = x + 1.$

a) Tính $\mathop {\lim }\limits_{x \to 1} f\left( x \right)$ và $\mathop {\lim }\limits_{x \to 1} g\left( x \right).$

b) Tính $\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right]$và so sánh $\mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right).$

c) Tính $\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right]$và so sánh $\mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right).$

d) Tính $\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right]$và so sánh $\mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right).$

e) Tính $\mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}}$và so sánh $\frac{{\mathop {\lim }\limits_{x \to 1} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 1} g\left( x \right)}}.$

Phương pháp giải:

$\mathop {\lim }\limits_{x \to {x_0}} x = {x_0};\mathop {\lim }\limits_{x \to {x_0}} c = c$

Lời giải chi tiết:

a) $\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} - 1} \right) = \mathop {\lim }\limits_{x \to 1} {x^2} - \mathop {\lim }\limits_{x \to 1} 1 = {1^2} - 1 = 0$

$\mathop {\lim }\limits_{x \to 1} g\left( x \right) = \mathop {\lim }\limits_{x \to 1} \left( {x + 1} \right) = \mathop {\lim }\limits_{x \to 1} x + \mathop {\lim }\limits_{x \to 1} 1 = 1 + 1 = 2$

b) $\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} + x} \right) = {1^2} + 1 = 2\\\mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right) = 0 + 2 = 2\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right).\end{array}$

c) $\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} - x - 2} \right) = {1^2} - 1 - 2 =  - 2\\\mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right) = 0 - 2 =  - 2\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right).\end{array}$

d) $\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left[ {\left( {{x^2} - 1} \right)\left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left( {{x^3} + {x^2} - x - 1} \right) = {1^3} + {1^2} - 1 - 1 = 0\\\mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right) = 0.2 = 0\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right).\end{array}$

e) $\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{x + 1}} = \mathop {\lim }\limits_{x \to 1} \left( {x - 1} \right) = 1 - 1 = 0\\\frac{{\mathop {\lim }\limits_{x \to 1} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 1} g\left( x \right)}} = \frac{0}{2} = 0\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{\mathop {\lim }\limits_{x \to 1} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 1} g\left( x \right)}}.\end{array}$

Luyện tập, vận dụng 2

Tính:

a) $\mathop {\lim }\limits_{x \to 2} \left[ {\left( {x + 1} \right)\left( {{x^2} + 2x} \right)} \right];$                         

b) $\mathop {\lim }\limits_{x \to 2} \sqrt {{x^2} + x + 3} .$

Phương pháp giải:

Sử dụng định lí về phép toán trên giới hạn hữu hạn của hàm số

Nếu $\mathop {\lim }\limits_{x \to {x_0}} f(x) = L$và $\mathop {\lim }\limits_{x \to {x_0}} g(x) = M$$\left( {L,M \in \mathbb{R}} \right)$thì

$\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x) \pm g(x)} \right] = L \pm M$

$\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x).g(x)} \right] = L.M$

$\mathop {\lim }\limits_{x \to {x_0}} \left[ {\frac{{f(x)}}{{g(x)}}} \right] = \frac{L}{M}\left( {M \ne 0} \right)$

Nếu $f(x) \ge 0$với mọi $x \in \left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}$ và $\mathop {\lim }\limits_{x \to {x_0}} f(x) = L$ thì $L \ge 0$và $\mathop {\lim }\limits_{x \to {x_0}} \sqrt {f(x)}  = \sqrt L$.

Lời giải chi tiết:

a) $\mathop {\lim }\limits_{x \to 2} \left[ {\left( {x + 1} \right)\left( {{x^2} + 2x} \right)} \right] = \mathop {\lim }\limits_{x \to 2} \left( {x + 1} \right).\mathop {\lim }\limits_{x \to 2} \left( {{x^2} + 2x} \right) = \left( {2 + 1} \right).\left( {{2^2} + 2.2} \right) = 24$                

b) $\mathop {\lim }\limits_{x \to 2} \sqrt {{x^2} + x + 3}  = \sqrt {\mathop {\lim }\limits_{x \to 2} \left( {{x^2} + x + 3} \right)}  = \sqrt {\mathop {\lim }\limits_{x \to 2} {x^2} + \mathop {\lim }\limits_{x \to 2} x + \mathop {\lim }\limits_{x \to 2} 3}  = \sqrt {{2^2} + 2 + 3}  = 3$

Hoạt động 3

Cho hàm số $f\left( x \right) = \left\{ \begin{array}{l} - 1,\,\,x < 0\\0,\,\,x = 0\\1,\,\,x > 0\end{array} \right.$

Hàm số $f\left( x \right)$ có đồ thị ở Hình 6.

a) Xét dãy số $\left( {{u_n}} \right)$ sao cho ${u_n} < 0$ và $\lim {u_n} = 0.$ Xác định $f\left( {{u_n}} \right)$ và tìm $\lim f\left( {{u_n}} \right).$

b) Xét dãy số $\left( {{v_n}} \right)$ sao cho ${v_n} > 0$ và $\lim {v_n} = 0.$ Xác định $f\left( {{v_n}} \right)$ và tìm $\lim f\left( {{v_n}} \right).$

Phương pháp giải:

Quan sát đồ thị hình 6 để trả lời câu hỏi.

Lời giải chi tiết:

a) Xét dãy số $\left( {{u_n}} \right)$ sao cho ${u_n} < 0$ và $\lim {u_n} = 0.$ Khi đó $f\left( {{u_n}} \right) =  - 1$ và $\lim f\left( {{u_n}} \right) =  - 1.$

b) Xét dãy số $\left( {{v_n}} \right)$ sao cho ${v_n} > 0$ và $\lim {v_n} = 0.$ Khi đó $f\left( {{v_n}} \right) = 1$ và $\lim f\left( {{v_n}} \right) = 1.$

Luyện tập, vận dụng 3

Tính $\mathop {\lim }\limits_{x \to  - {4^ + }} \left( {\sqrt {x + 4}  + x} \right)$

Phương pháp giải:

Sử dụng định nghĩa giới hạn một phía.

- Cho hàm số $y = f(x)$xác định trên khoảng $\left( {a;{x_0}} \right)$. Số L được gọi là giới hạn bên trái của hàm số $y = f(x)$khi $x \to {x_0}$ nếu với dãy số $\left( {{x_n}} \right)$bất kì thỏa mãn $a < {x_n} < {x_0}$ và ${x_n} \to {x_0}$ta có $f({x_n}) \to L$, kí hiệu $\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = L$.

- Cho hàm số $y = f(x)$xác định trên khoảng $\left( {{x_0};b} \right)$. Số L là giới hạn bên của hàm số $y = f(x)$ khi $x \to {x_0}$ nếu với dãy số $\left( {{x_n}} \right)$bất kì thỏa mãn ${x_0} < {x_n} < b$ và ${x_n} \to {x_0}$ta có $f({x_n}) \to L$, kí hiệu $\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L$.

Lời giải chi tiết:

Với dãy số $\left( {{x_n}} \right)$ bất kì ${x_n} >  - 4$ và ${x_n} \to  - 4,$ ta có:

$\begin{array}{c}\mathop {\lim }\limits_{{x_n} \to  - {4^ + }} \left( {\sqrt {{x_n} + 4}  + {x_n}} \right) = \mathop {\lim }\limits_{{x_n} \to  - {4^ + }} \sqrt {{x_n} + 4}  + \mathop {\lim }\limits_{{x_n} \to  - {4^ + }} {x_n} = \sqrt {\mathop {\lim }\limits_{{x_n} \to  - {4^ + }} \left( {{x_n} + 4} \right)}  + \left( { - 4} \right)\\ = \sqrt {\mathop {\lim }\limits_{{x_n} \to  - {4^ + }} {x_n} + 4}  - 4 = \sqrt { - 4 + 4}  - 4 =  - 4\end{array}$

Vậy $\mathop {\lim }\limits_{x \to  - {4^ + }} \left( {\sqrt {x + 4}  + x} \right) =  - 4$