Lý thuyết Dấu của tam thức bậc hai - SGK Toán 10 Kết nối tri thức

A. Lý thuyết

1. Dấu của tam thức bậc hai

a) Khái niệm tam thức bậc hai

Chú ý: Nghiệm của phương trình bậc hai $a{x^2} + bx + c = 0$ cũng được gọi là nghiệm của tam thức bậc hai $a{x^2} + bx + c$.

b) Dấu của tam thức bậc hai

Mối quan hệ giữa dấu của tam thức bậc hai $a{x^2} + bx + c$ với dấu của hệ số a trong từng trường hợp của $\Delta$ được phát biểu trong định lí về dấu của tam thức bậc hai sau đây:

Chú ý: Trong định lí về dấu của tam thức bậc hai, có thể thay $\Delta$ bởi $\Delta '$.

2. Bất phương trình bậc hai

Nhận xét: Để giải bất phương trình bậc hai $a{x^2} + bx + c > 0$ (hoặc $a{x^2} + bx + c \ge 0$, $a{x^2} + bx + c < 0$, $a{x^2} + bx + c \le 0$) ta cần xét dấu tam thức $a{x^2} + bx + c$, từ đó suy ra tập nghiệm.

B. Bài tập

Bài 1: Hãy cho biết biểu thức nào sau đây là tam thức bậc hai?

A. $3x + 2\sqrt x  + 1$

B. $- 5{x^4} + 3{x^2} + 4$

C. $- \frac{2}{3}{x^2} + 7x - 4$

D. ${\left( {\frac{1}{x}} \right)^2} + 2\frac{1}{x} + 3$

Giải:

$- \frac{2}{3}{x^2} + 7x - 4$ là tam thức bậc hai với $a =  - \frac{2}{3},b = 7,c =  - 4$.

Bài 2: Xét dấu các tam thức bậc hai sau đây:

a) ${x^2} + x + 1$.

b) $- \frac{3}{2}{x^2} + 9x - \frac{{27}}{2}$.

c) $2{x^2} + 6x - 8$.

Giải:

a) $f(x) = {x^2} + x + 1$ có $\Delta  =  - 3 < 0$ và $a = 1 > 0$ nên f(x) > 0 với mọi $x \in \mathbb{R}$.

b)

$f(x) =  - \frac{3}{2}{x^2} + 9x - \frac{{27}}{2}$ có $\Delta  = 0$ và $a =  - \frac{3}{2} < 0$ nên f(x) có nghiệm kép x = 3 và f(x) < 0 với mọi $x \ne 3$.

c) Dễ thấy $f(x) = 2{x^2} + 6x - 8$ có $\Delta ' = 25 > 0$, a = 2 > 0 và có hai nghiệm phân biệt ${x_1} =  - 4$, ${x_2} = 1$. Do đó ta có bảng xét dấu:

Suy ra f(x) > 0 với mọi $x \in ( - \infty ; - 4) \cup (1; + \infty )$ và f(x) < 0 với mọi $x \in ( - 4;1)$.

Bài 3: Giải các bất phương trình sau:

a) $3{x^2} + x + 5 \le 0$.

b) $- 3{x^2} + 2\sqrt 3 x - 1 \ge 0$.

c) $- {x^2} + 2x + 1 > 0$.

Giải:

a) Tam thức $f(x) = 3{x^2} + x + 5$ có $\Delta  =  - 59 < 0$, hệ số a = 3 > 0 0 nên f(x) luôn dương (cùng dấu với a) với mọi x, tức là $3{x^2} + x + 5 > 0$ với mọi $x \in \mathbb{R}$. Suy ra bất phương trình vô nghiệm.

b) Tam thức $f(x) =  - 3{x^2} + 2\sqrt 3 x - 1$ có $\Delta ' = 0$, hệ số a = -3 < 0 nên f(x) có nghiệm kép $x = \frac{{\sqrt 3 }}{3}$ và f(x) luôn âm (cùng dấu với a) với mọi $x \ne \frac{{\sqrt 3 }}{3}$, tức là $- 3{x^2} + 2\sqrt 3 x - 1 < 0$ với mọi $x \ne \frac{{\sqrt 3 }}{3}$.

Suy ra bất phương trình có nghiệm duy nhất $x = \frac{{\sqrt 3 }}{3}$.

c) Tam thức $f(x) =  - {x^2} + 2x + 1$ có $\Delta ' = 2 > 0$ nên f(x) có hai nghiệm ${x_1} = 1 - \sqrt 2$ và ${x_2} = 1 + \sqrt 2$.

Mặt khác, a = -1 < 0, do đó ta có bảng xét dấu sau:

Tập nghiệm của bất phương trình là $S 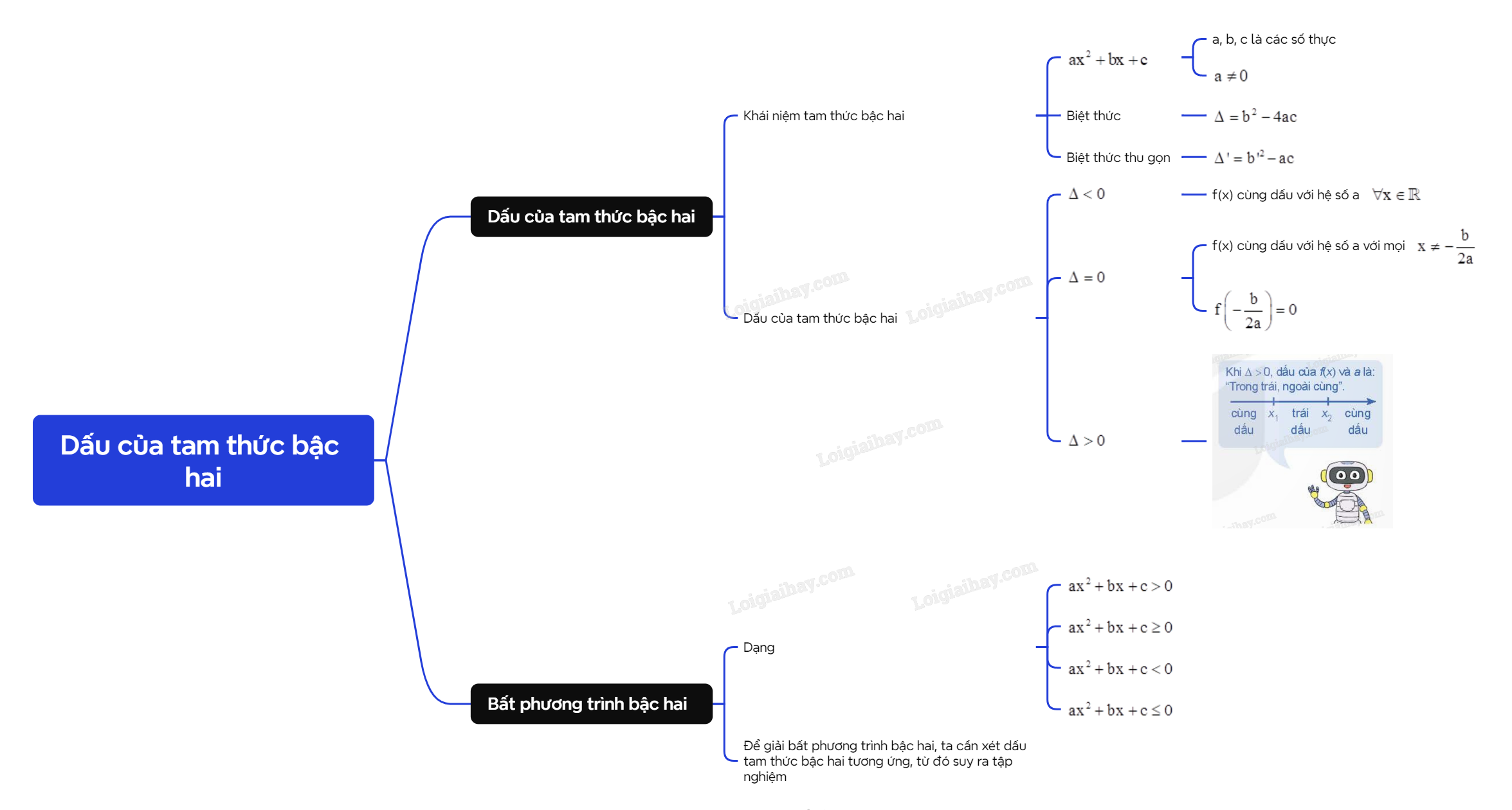= \left( {1 - \sqrt 2 ;1 + \sqrt 2 } \right)$.