Giải mục 1 trang 19, 20, 21, 22 SGK Toán 10 tập 2 - Kết nối tri thức

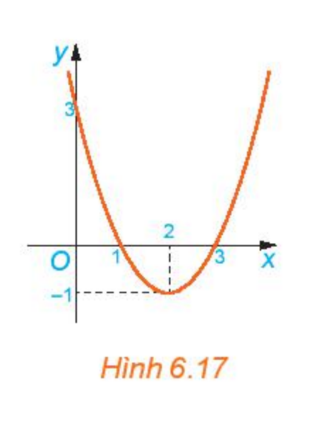
HĐ1

Hãy chỉ ra một đặc điểm chung của các biểu thức dưới đây:

$A = 0,5{x^2}$    

$B = 1 - {x^2}$   

$C = {x^2} + x + 1$     

$D = (1 - x)(2x + 1)$

Lời giải chi tiết:

Ta có :

$A = 0,5{x^2}$

$B = 1 - {x^2}$

$C = {x^2} + x + 1$

$D = (1 - x)(2x + 1) = 2x + 1 - 2{x^2} - x =  - 2{x^2} + x + 1$

=> Các biểu thức đều có dạng $a{x^2} + bx + c(a \ne 0)$_{, a,b,c là các số thực.}

Luyện tập 1

Hãy cho biết biểu thức nào sau đây là tam thức bậc hai.

$A = 3x + 2\sqrt x  + 1$ 

$B =  - 5{x^4} - 3{x^2} + 4$

$C =  - \frac{2}{3}{x^2} + 7x - 4$

$D = {\left( {\frac{1}{x}} \right)^2} + 2.\frac{1}{x} + 3$

Phương pháp giải:

Tam thức bậc hai là biểu thức có dạng $a{x^2} + bx + c$, trong đó a,b,c là những số cho trước $\left( {a \ne 0} \right)$

Lời giải chi tiết:

Biểu thức $C =  - \frac{2}{3}{x^2} + 7x - 4$ là tam thức bậc hai

Biểu thức A không là tam thức bậc hai vì chứa $\sqrt x$

Biểu thức B không là tam thức bậc hai vì chứa ${x^4}$

Biểu thức D không là tam thức bậc hai vì chứa ${\left( {\frac{1}{x}} \right)^2}$

HĐ2

Cho hàm số bậc hai $y = f(x) = {x^2} - 4x + 3$

a) Xác định hệ số a. Tính $f(0);f(1);f(2);f(3);f(4)$ và nhận xét về dấu của chúng so với dấu của hệ số a

b) Cho đồ thị hàm số y=f(x) (H.6.17). Xét từng khoảng $\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)$, đồ thị nằm phía trên hay phía dưới trục Ox?

c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.

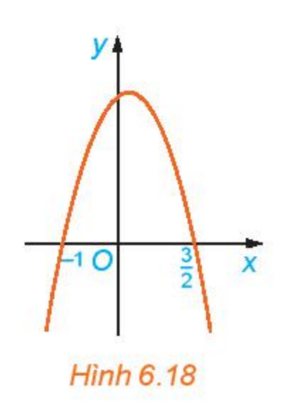
Lời giải chi tiết:

a) Hệ số a là: a=1

$f(0) = {0^2} - 4.0 + 3 = 3$

$f(1) = {1^2} - 4.1 + 3 = 0$

$f(2) = {2^2} - 4.2 + 3 =  - 1$

$f(3) = {3^2} - 4.3 + 3 = 0$

$f(4) = {4^2} - 4.4 + 3 = 3$

=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a

b) Nhìn vào đồ thị ta thấy

- Trên khoảng $\left( { - \infty ;1} \right)$ đồ thị nằm phía trên trục hoành

- Trên khoảng $\left( {1;3} \right)$, đồ thị nằm phía dưới trục hoành

- Trên khoảng $\left( {3; + \infty } \right)$, đồ thị nằm phía trên trục hoành

c) - Trên khoảng $\left( { - \infty ;1} \right)$ đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a

- Trên khoảng $\left( {1;3} \right)$, đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a

- Trên khoảng $\left( {3; + \infty } \right)$, đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a

HĐ3

Cho đồ thị hàm số $y = g(x) =  - 2{x^3} + x + 3$ như Hình 6.18

a) Xét trên từng khoảng $\left( { - \infty ; - 1} \right),\left( { - 1;\frac{3}{2}} \right),\left( {\frac{3}{2}; + \infty } \right)$, đồ thị nằm phía trên trục Ox hay nằm phía dưới trục Ox

b) Nhận xét về dấu của g(x) và dấu của hệ số a trên từng khoảng đó

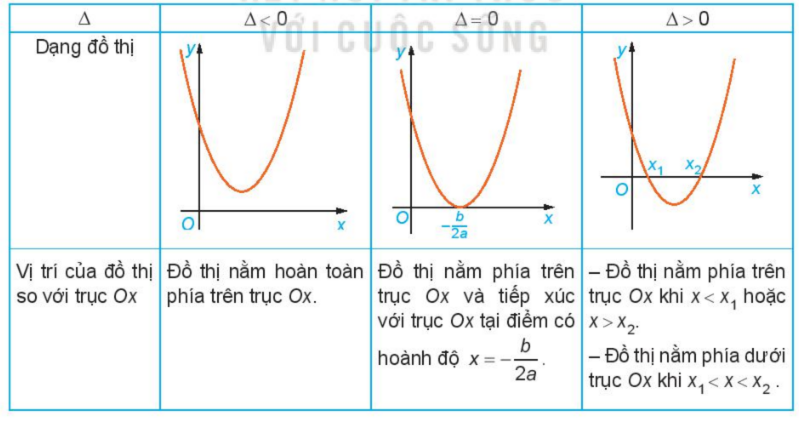
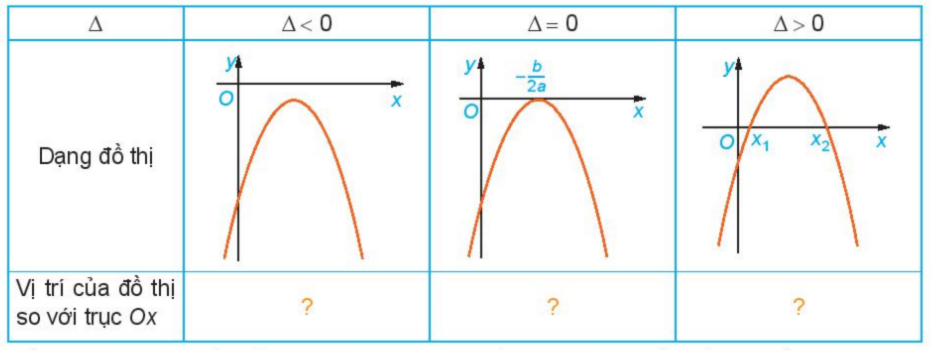
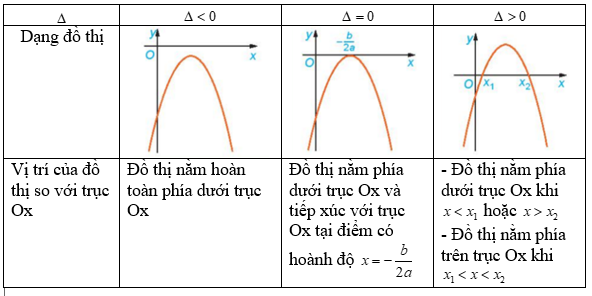
Lời giải chi tiết:

Ta có: hệ số a=-2<0

a) Nhìn vào đồ thị ta thấy

- Trên khoảng $\left( { - \infty ; - 1} \right)$ đồ thị nằm phía dưới trục hoành

- Trên khoảng $\left( { - 1;\frac{3}{2}} \right)$, đồ thị nằm phía trên trục hoành

- Trên khoảng $\left( {\frac{3}{2}; + \infty } \right)$, đồ thị nằm phía dưới trục hoành

c) - Trên khoảng $\left( { - \infty ; - 1} \right)$ đồ thị nằm phía dưới trục hoành => f(x)<0, cùng dầu với hệ số a

- Trên khoảng $\left( { - 1;\frac{3}{2}} \right)$, đồ thị nằm phía trên trục hoành => f(x) >0, khác dấu với hệ số a

- Trên khoảng $\left( {\frac{3}{2}; + \infty } \right)$, đồ thị nằm phía dưới trục hoành => f(x)<0, cùng dấu với hệ số a

HĐ4

Nêu nội dung thay vào các ô có dấu “?” trong bảng sau cho thích hợp

Trường hợp a>0

Trường hợp a<0

Lời giải chi tiết:

Luyện tập 2

Xét dấu các tam thức bậc hai sau:

a) $- 3{x^2} + x - \sqrt 2$ 

b) ${x^2} + 8x + 16$ 

c) $- 2{x^2} + 7x - 3$

Phương pháp giải:

Xét dấu tam thức bậc hai $f(x) = a{x^2} + bx + c$

Bước 1: Tính $\Delta  = {b^2} - 4ac$

Bước 2:

-  Nếu $\Delta  < 0$ thì $f(x)$ luôn cùng dấu với a với mọi $x \in \mathbb{R}$

-  Nếu $\Delta  = 0$ thì $f(x)$có nghiệm kép là  ${x_0}$ . Vậy $f(x)$cùng dấu với a với $x \ne {x_0}$

-  Nếu $\Delta  > 0$ thì $f(x)$có 2 nghiệm là ${x_1};{x_2}$$({x_1} < {x_2})$. Ta lập bảng xét dấu.

Lời giải chi tiết:

a) $f(x) =  - 3{x^2} + x - \sqrt 2$có $\Delta  = 1 - 12\sqrt 2  < 0$và a=-3<0 nên $f(x) < 0$với mọi $x \in \mathbb{R}$

b) $g(x) = {x^2} + 8x + 16$ có $\Delta  = 0$và a=1>0 nên g(x) có nghiệm kép $x =  - 4$ và g(x) >0 với mọi $x \ne  - 4$

c) $h(x) =  - 2{x^2} + 7x - 3$ có $\Delta  = 25$>0 và a=-2<0 và có 2 nghiệm phân biệt ${x_1} = \frac{1}{2};{x_2} = 3$

Do đó ta có bảng xét dấu h(x)

Suy ra h(x) <0 với mọi $x \in \left( { - \infty ;\frac{1}{2}} \right) \cup \left( {3; + \infty } \right)$ và h(x)>0 với mọi $x \in \left( {\frac{1}{2};3} \right)$