Giải mục 4 trang 35,36 SGK Toán 12 tập 2 - Kết nối tri thứcĐIỀU KIỆN ĐỂ HAI MẶT PHẲNG VUÔNG GÓC VỚI NHAU Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Hoá - Sinh - Sử - Địa
Lựa chọn câu để xem lời giải nhanh hơn
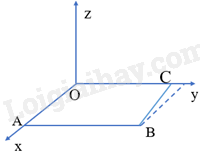
HĐ8 Trả lời câu hỏi Hoạt động 8 trang 35 SGK Toán 12 Kết nối tri thức Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với hai vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng. a) Góc giữa hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\) và góc giữa hai giá của \(\overrightarrow n ,\overrightarrow {n'} \) có mối quan hệ gì? b) Hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) vuông góc với nhau khi và chỉ khi hai vectơ pháp tuyến \(\overrightarrow n ,\overrightarrow {n'} \) có mối quan hệ gì? Phương pháp giải: Sử dụng kiến thức về góc giữa hai mặt phẳng: Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng bất kì tương ứng vuông góc với hai mặt phẳng đó. Lời giải chi tiết: a) Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng bất kì tương ứng vuông góc với hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\). Mà giá của \(\overrightarrow n \) vuông góc với mặt phẳng \(\left( \alpha \right)\), giá của \(\overrightarrow {n'} \) vuông góc với mặt phẳng \(\left( \beta \right)\). Do đó, góc giữa hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\) bằng góc giữa hai giá của \(\overrightarrow n ,\overrightarrow {n'} \). b) Hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) vuông góc với nhau khi và chỉ khi góc giữa hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) bằng \({90^o}\), do đó, hai vectơ pháp tuyến \(\overrightarrow n ,\overrightarrow {n'} \) vuông góc với nhau. LT9 Trả lời câu hỏi Luyện tập 9 trang 36 SGK Toán 12 Kết nối tri thức Trong không gian Oxyz, hai mặt phẳng sau đây có vuông góc với nhau hay không? \(\left( \alpha \right):3x + y - z + 1 = 0,\left( \beta \right):9x + 3y - 3z + 3 = 0\). Phương pháp giải: Sử dụng kiến thức về điều kiện để hai mặt phẳng vuông góc để chứng minh: Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với hai vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng. Khi đó, \(\left( \alpha \right) \bot \left( \beta \right) \Leftrightarrow \overrightarrow n \bot \overrightarrow {n'} \Leftrightarrow AA' + BB' + CC' = 0\). Lời giải chi tiết: Mặt phẳng \(\left( \alpha \right)\) có 1 vectơ pháp tuyến là \(\overrightarrow {{n_1}} \left( {3;1; - 1} \right)\), mặt phẳng \(\left( \beta \right)\) có 1 vectơ pháp tuyến là \(\overrightarrow {{n_2}} \left( {9;3; - 3} \right)\). Ta có: \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 3.9 + 1.3 + 3.1 = 33 \ne 0\) nên hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) không vuông góc với nhau. VD3 Trả lời câu hỏi Vận dụng 3 trang 36 SGK Toán 12 Kết nối tri thức Trong không gian Oxyz, sàn của một căn phòng có dạng hình tứ giác với bốn đỉnh O(0; 0; 0), A(2; 0; 0), B(2; 3; 0), \(C\left( {0;2\sqrt 2 ;0} \right)\). Bốn bức tường của căn phòng đều vuông góc với sàn. a) Viết phương trình bốn mặt phẳng tương ứng chứa bốn bức tường đó. b) Trong bốn mặt phẳng tương ứng chứa bốn bức tường đó, hãy chỉ ra những cặp mặt phẳng vuông góc với nhau.
Phương pháp giải: Sử dụng kiến thức về lập phương trình mặt phẳng đi qua một điểm và biết cặp vectơ chỉ phương: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vectơ chỉ phương \(\overrightarrow u ,\overrightarrow v \) có thể thực hiện theo các bước sau: + Tìm vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\). + Lập phương trình tổng quát của mặt phẳng đi qua M và biết vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\). Lời giải chi tiết:
a) Bốn mặt phẳng tương ứng chứa bốn bức tường vuông góc với mặt sàn là: Mặt phẳng (Oyz), mặt phẳng (Oxz), mặt phẳng (P) chứa hai điểm A, B và vuông góc với mặt sàn, mặt phẳng (Q) chứa hai điểm B, C và vuông góc với mặt sàn. Mặt phẳng (Oyz) có vectơ pháp tuyến \(\overrightarrow i \left( {1;0;0} \right)\) và đi qua điểm \(O\left( {0;0;0} \right)\) nên phương trình mặt phẳng (Oyz) là: \(x = 0\) Mặt phẳng (Oxz) có vectơ pháp tuyến \(\overrightarrow j \left( {0;1;0} \right)\) và đi qua điểm \(O\left( {0;0;0} \right)\) nên phương trình mặt phẳng (Oxz) là: \(y = 0\) Ta có: \(\overrightarrow {AB} \left( {0;3;0} \right),\overrightarrow {BC} \left( { - 2;2\sqrt 2 - 3;0} \right),\overrightarrow i \left( {1;0;0} \right),\overrightarrow j \left( {0;1;0} \right),\overrightarrow k \left( {0;0;1} \right)\) Mặt phẳng (P) đi qua điểm A(2; 0; 0) và nhận \(\overrightarrow i = \left( {1;0;0} \right)\) làm vectơ pháp tuyến. Do đó, phương trình mặt phẳng (P) là: \(x - 2 = 0\) \(\left[ {\overrightarrow {BC} ,\overrightarrow k } \right] = \left( {\left| {\begin{array}{*{20}{c}}{2\sqrt 2 - 3}&0\\0&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - 2}\\1&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&{2\sqrt 2 - 3}\\0&0\end{array}} \right|} \right) = \left( {2\sqrt 2 - 3;2;0} \right)\) Mặt phẳng (Q) đi qua điểm \(C\left( {0;2\sqrt 2 ;0} \right)\) và nhận \(\left[ {\overrightarrow {BC} ,\overrightarrow k } \right] = \left( {2\sqrt 2 - 3;2;0} \right)\) làm vectơ pháp tuyến. Do đó, phương trình mặt phẳng (Q) là: \(\left( {2\sqrt 2 - 3} \right)x + 2\left( {y - 2\sqrt 2 } \right) = 0 \Leftrightarrow \left( {2\sqrt 2 - 3} \right)x + 2y - 4\sqrt 2 = 0\) b) Các cặp mặt phẳng vuông góc với nhau là: (Oxz) và (Oyz); (Oxz) và (P).
|