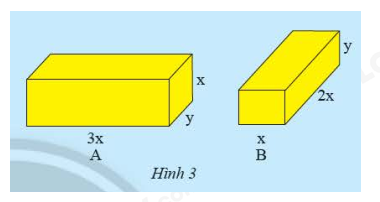
Giải mục 3 trang 9 SGK Toán 8 tập 1– Chân trời sáng tạo

HĐ3

Cho hai hình hộp chữ nhật A và B có các kích thước như hình 3.

a) Tính tổng thể tích của hình hộp chữ nhật A và B.

b) Viết biểu thức biểu diễn sự chênh lệch thể tích của A và B.

Phương pháp giải:

Thể tích hình hộp chữ nhật là lượng không gian mà hình chiếm, được tính bằng tích của diện tích đáy và chiều cao: \(V = a.b.h\), trong đó \(a\), \(b\), \(h\), \(V\) lần lượt là chiều dài, chiều rộng, chiều cao và thể tích của hình hộp chữ nhật.

Lời giải chi tiết:

a) Thể tích của hình hộp chữ nhật A là: \({V_A} = 3x.y.x = 3.{x^2}y\)

Thể tích của hình hộp chữ nhật B là: \({V_B} = 2x.x.y = 2{x^2}y\)

Tổng thể tích của hình hộp chữ nhật A và B là: \(3{x^2}y + 2{x^2}y = \left( {3 + 2} \right).{x^2}y = 5{x^2}y\)

b) Biểu thức biểu diễn sự chênh lệch thể tích của A và B là: \(3{x^2}y - 2{x^2}y = \left( {3 - 2} \right).{x^2}y = {x^2}y\)

Thực hành 3

Mỗi cặp đơn thức sau có đồng dạng không? Nếu có, hãy tìm tổng và hiệu của chúng.

a) \(xy\) và \( - 6xy\)              

b) \(2xy\) và \(x{y^2}\)                                  

c) \( - 4yz{x^2}\) và \(4{x^2}yz\)

Phương pháp giải:

Hai đơn thức đồng dạng là hai đơn thức có hệ số khác \(0\) và có cùng phần biến

Để cộng, trừ (hay tìm tổng, hiệu) hai đơn thức đồng dạng, ta cộng, trừ hệ số của chúng là giữ nguyên phần biến.

Lời giải chi tiết:

a) \(xy\) và \( - 6xy\) là hai đơn thức đồng dạng vì có hệ số khác \(0\) và có cùng phần biến là \(xy\).

Ta có:

\(xy + \left( { - 6xy} \right) = xy - 6xy = \left( {1 - 6} \right)xy =  - 5xy\)

\(xy - \left( { - 6xy} \right) = xy + 6xy = \left( {1 + 6} \right)xy = 7xy\)

b) \(2xy\) và \(x{y^2}\)           không là hai đơn thức đồng dạng.

c) \( - 4yz{x^2}\) và \(4{x^2}yz\) là hai đơn thức đồng dạng vì có hệ số khác 0 và có cùng phần biến là \({x^2}yz\).

Ta có:

\( - 4yz{x^2} + 4{x^2}yz = \left( { - 4 + 4} \right){x^2}yz = 0\)

\( - 4yz{x^2} - 4{x^2} = \left( { - 4 - 4} \right){x^2}yz =  - 8{x^2}yz\)