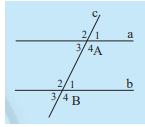
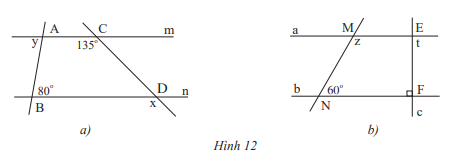
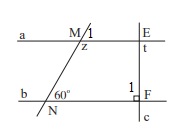
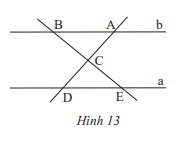
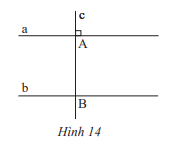
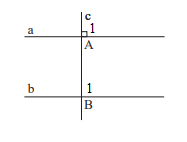
Giải mục 3 trang 79, 80 SGK Toán 7 tập 1 - Chân trời sáng tạo

HĐ 3

Em hãy:

- Vẽ hai đường thẳng a và b song song với nhau.

- Vẽ đường thẳng c cắt đường thẳng a và b lần lượt tại A và B.

a) Chọn và đo một cặp góc so le trong, so sánh cặp góc này.

b) Chọn và đo một cặp góc đồng vị, so sánh cặp góc này.

Phương pháp giải:

Vẽ hình.

Đo và nhận xét

Lời giải chi tiết:

a) Một cặp góc so le trong là góc A₃ và góc B₁ . Hai góc này cùng có số đo là 60 $^\circ$ nên chúng bằng nhau .

b) Một cặp góc đồng vị là góc A₁ và góc B₁ . Hai góc này cùng có số đo là 60 $^\circ$ nên chúng bằng nhau .

Thực hành 4

Cho biết m // n và a // b. Tính số đo x,y,z và t của các góc trong hình 12.

Phương pháp giải:

Sử dụng tính chất của 2 đường thẳng song song:

Một đường thẳng cắt hai đường thẳng song song thì:

+ 2 góc so le trong bằng nhau

+ 2 góc đồng vị bằng nhau

Lời giải chi tiết:

a) Vì m // n nên x = 135$^\circ$( 2 góc đồng vị) ; y = 80$^\circ$ ( 2 góc so le trong)

b)

Vì a // b nên $\widehat {{M_1}} = 60^\circ$ ( 2 góc đồng vị)

Mà $\widehat {{M_1}} + z = 180^\circ$ ( 2 góc kề bù) nên z = 180$^\circ$- 60$^\circ$=120$^\circ$

Vì a // b nên $\widehat {{F_1}} = t$ ( 2 góc so le trong), mà $\widehat {{F_1}} = 90^\circ$ nên t = 90$^\circ$

Vận dụng 1

Tìm các cặp góc bằng nhau của hai tam giác ABC và DEC trong Hình 13, biết a // b.

Phương pháp giải:

*2 góc đối đỉnh thì bằng nhau

*Sử dụng tính chất của 2 đường thẳng song song: Một đường thẳng cắt hai đường thẳng song song thì:

+ 2 góc so le trong bằng nhau

+ 2 góc đồng vị bằng nhau.

Lời giải chi tiết:

Vì a // b nên $\widehat {BAC} = \widehat {CDE};\widehat {ABC} = \widehat {CED}$ (2 góc so le trong)

Ta có: $\widehat {ACB} = \widehat {DCE}$ ( 2 góc đối đỉnh).

Vận dụng 2

Cho hai đường thẳng a, b song song với nhau, đường thẳng c vuông góc với a tại A và cắt b tại B. Hãy giải thích tại sao đường thẳng c cũng vuông góc với b.

Phương pháp giải:

Sử dụng tính chất của 2 đường thẳng song song: Một đường thẳng cắt hai đường thẳng song song thì 2 góc đồng vị bằng nhau.

Lời giải chi tiết:

Vì a //  b nên $\widehat {{B_1}} = \widehat {{A_1}}$ (2 góc đồng vị), mà $\widehat {{A_1}} = 90^\circ$ nên $\widehat {{B_1}} = 90^\circ$.

Vậy c vuông góc với b.