Giải mục 2 trang 9, 10, 11, 12 Chuyên đề học tập Toán 12 - Kết nối tri thứcGiả sử số vụ vi phạm Luật Giao thông trên một đoạn đường AB trong 98 buổi tối thứ Bảy được thống kê như sau: 10 tối không có vụ nào; 20 tối có 1 vụ; 23 tối có 2 vụ; 25 tối có 3 vụ; 15 tối có 4 vụ; 5 tối có 7 vụ. Hỏi trung bình có bao nhiêu vụ vi phạm Luật Giao thông trên đoạn đường B trong 98 buổi tối thứ Bảy đó? Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Hoá - Sinh - Sử - Địa
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 3 Trả lời câu hỏi Hoạt động 3 trang 9 Chuyên đề học tập Toán 12 Kết nối tri thức Giả sử số vụ vi phạm Luật Giao thông trên một đoạn đường AB trong 98 buổi tối thứ Bảy được thống kê như sau: 10 tối không có vụ nào; 20 tối có 1 vụ; 23 tối có 2 vụ; 25 tối có 3 vụ; 15 tối có 4 vụ; 5 tối có 7 vụ. Hỏi trung bình có bao nhiêu vụ vi phạm Luật Giao thông trên đoạn đường B trong 98 buổi tối thứ Bảy đó? Phương pháp giải: Trung bình = Tổng số vụ tai nạn / số buổi tối thứ Bảy Lời giải chi tiết: Có: 0.10+1.20+2.23+3.25+4.15+7.5=236 vụ vi phạm trong 98 buổi tối thứ Bảy Vậy trung bình có 23698≈2,408 vụ vi phạm trọng 98 buổi tối thứ Bảy Luyện tập 2 Trả lời câu hỏi Luyện tập 2 trang 10 Chuyên đề học tập Toán 12 Kết nối tri thức Giả sử số vụ vi phạm Luật Giao thông trên một đoạn đường vào tối thứ Bảy có thể là 0; 1; 2; 3; 4; 5 với các xác suất tương ứng là 0,1; 0,2; 0,25; 0,15 và 0,05. Hỏi trung bình có bao nhiêu vụ vi phạm Luật Giao thông trên đoạn đường đó và tối thứ Bảy? Phương pháp giải: Bước 1: Dựa vào dữ kiện đề bài lập bảng phân bố xác suất của biến ngẫn nhiên X Bước 2: Tính kì vọng E(X) theo công thức Lời giải chi tiết: Gọi X là số vụ vi phạm Luật Giao thông đường bộ trên đoạn đường vào tối thứ Bảy. Khi đó, X là biến ngẫu nhiên rời rạc có bảng phân bố xác suất:
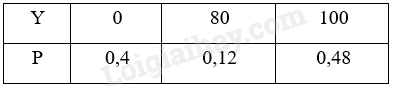
Ta có: E(X)=0,01+1.0,2+2.0,25+3.0,25+4.0,15+5.0,05=2,3 Vậy trên đoạn đường vào tối thứ Bảy có trung bình 2,3 vụ vi phạm Luật Giao thông đường bộ Vận dụng 2 Trả lời câu hỏi Vận dụng 2 trang 11 Chuyên đề học tập Toán 12 Kết nối tri thức Tiếp tục xét tình huống mở đầu, giả sử ở vòng 1 Minh chọn câu hỏi loại II. a) Hỏi trung bình Minh nhận được bao nhiêu điểm? b) Ở vòng 1 Minh nên chọn loại câu hỏi nào? Phương pháp giải: Bước 1: Dựa vào dữ kiện đề bài lập bảng phân bố xác suất của biến ngẫn nhiên Y. Bước 2: Tính kì vọng E(Y) theo công thức. Bước 3: So sánh E(X) với E(Y) và đưa ra kết luận. Lời giải chi tiết: a) Giả sử ở vòng 1 Minh chọn câu hỏi loại II. Gọi Y là số điểm Minh nhận được. Gọi A là biến cố “Minh trả lời đúng câu hỏi loại I” ⇒P(A)=0,8 B là biến cố “Minh trả lời đúng câu hỏi loại II”. ⇒P(B)=0,6 + Nếu trả lời sai: Minh được 0 điểm. Cuộc chơi kết thúc tại đây Khi đó, P(Y=0)=P(¯B)=1−−P(B)=1−−0,6=0,4. + Nếu trả lời đúng Minh nhận 80 điểm và Minh sẽ bước vào vòng 2, bốc ngẫu nhiên một câu hỏi loại I. Nếu trả lời sai, Minh không có điểm và phải dừng cuộc chơi và số điểm với số điểm nhận được là 80 + 0 = 80 điểm. Theo giả thiết A và B là biến cố độc lập. Theo công thức nên xác suất cho hai biến cố độc lập ta có: P(Y=80)=P(B¯A)=P(B)P(¯A)=(0,6)(1−−0,8)=0,12 + Nếu trả lời đúng Minh nhận 80 điểm. Cuộc chơi kết thúc tại đây và Minh được 20 + 80 = 100 điểm. Theo công thức nhân xác suất cho hai biến cố độc lập ta có: P(Y=100)=P(BA)=P(B)P(A)=0,6.0,8=0,48 Bảng phân bố xác suất của Y là:
Ta có: E(Y)=0.0,4+80.0,12+100.0,48=57,6. Vậy trung bình Minh được 57,6 điểm b) Ta có E(X)=54,4, E(Y)=57,6. Ta thấy E(Y)>E(X) nên ở vòng 1, Minh nên chọn câu hỏi loại II. Hoạt động 4 Trả lời câu hỏi Hoạt động 4 trang 11 Chuyên đề học tập Toán 12 Kết nối tri thức Một nhà đầu tư xem xét hai phương án đầu tư. Với phương án 1 thì doanh thu một năm sẽ là 8 tỉ đồng hoặc 2 tỉ đồng với xác suất tương ứng là 13 và 23. Với phương án 2 thì doanh thu một năm sẽ là 5 tỉ đồng hoặc 3 tỉ đồng với hai xác suất bằng nhau. a) Hãy so sánh doanh thu trung bình của phương án 1 và phương án 2. b) Nhà đầu tư nên chọn phương án nào? Phương pháp giải: Bước 1: Dựa vào dữ kiện đề bài lập bảng phân bố xác suất của biến ngẫn nhiên X, Y. Bước 2: Tính kì vọng E(X),E(Y) theo công thức. Bước 3: So sánh E(X) với E(Y) và đưa ra kết luận. Lời giải chi tiết: a) Gọi X và Y tương ứng là doanh thu theo phương án 1 và phương án 2 Ta có bảng phân bố xác suất của biến ngẫu nhiên X và Y
Khi đó, E(X)=8.13+2.23=4; E(Y)=3.12+5.12=4. Ta thấy E(X)=E(Y) nên doanh thu trung bình của hai phương án bằng nhau. b) Phương án 1 nếu nhà đầu tư ưa mạo hiểm Phương án 2 nếu nhà đầu tư muốn sự an toàn Câu hỏi Trả lời câu hỏi trang 11 Chuyên đề học tập Toán 12 Kết nối tri thức Trở lại HĐ4. Gọi X và Y tương ứng là doanh thu theo phương án 1 và phương án 2. Tính độ lệch chuẩn của X và Y. Phương pháp giải: Áp dụng công thức tính độ lệch chuẩn Lời giải chi tiết: E(X)=4V(X)=(8−4)2.13+(2−4)2.23=8⇒σ(X)=√8≈2,828. E(Y)=4V(Y)=(5−4)2.12+(3−4)2.12=1⇒σ(Y)=1 Luyện tập 3 Trả lời câu hỏi Luyện tập 3 trang 12 Chuyên đề học tập Toán 12 Kết nối tri thức Cho biến ngẫu nhiên rời rạc X với bảng phân bố xác suất như sau:
a) Tính V(X) và σ(X) theo định nghĩa b) Tính V(X) theo công thức (2). Phương pháp giải: Áp dụng các công thức để tính. Lời giải chi tiết: a) E(X)=0.0,16+1.0,18+2.0,25+3.0,28+4.0,13=2,04. V(X)=(0−−2,04)2.0,16+(1−−2,04)2.0,18+(2−−2,04)2.0,25+(3−−2,04)2.0,28+(4−−2,04)2.0,13=1,6184.⇒σ(X)=√1,6184≈1,2722 b) V(X)=02.0,16+12.0,18+22.0,25+32.0,28+42.0,13−−(2,04)2=1,6184.
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
|