Giải mục 2 trang 8,9,10 SGK Toán 11 tập 1 - Kết nối tri thức

LT 3

a) Đổi từ độ sang rađian các số đo sau: ${360^ \circ }, - {450^ \circ }$

b) Đổi từ rađian sang độ các số đo sau: $3\pi , - \frac{{11\pi }}{5}$

Phương pháp giải:

Áp dụng công thức:

${\alpha ^ \circ } = \alpha .\frac{\pi }{{180}}rad$ ; $\alpha \,rad = \alpha .{\left( {\frac{{180}}{\pi }} \right)^ \circ }$

Lời giải chi tiết:

a) Ta có:

$\begin{array}{l}{360^ \circ } = 360.\frac{\pi }{{180}} = 2\pi \\ - {450^ \circ } = -450.\frac{\pi }{{180}} = -\frac{5}{2}\pi \end{array}$

b)$3\pi  = 3\pi .{\left( {\frac{{180}}{\pi }} \right)^ \circ } = {540^ \circ }$

$- \frac{{11\pi }}{5} = \left( { - \frac{{11\pi }}{5}} \right).{\left( {\frac{{180}}{\pi }} \right)^ \circ } =  - {396^ \circ }$

Quảng cáo

HĐ 3

Cho đường tròn bán kính R.

a) Độ dài của cung tròn có số đo bằng 1 rad là bao nhiêu

b) Tính độ dài l của cung tròn có số đo $\alpha$rad.

Phương pháp giải:

Áp dụng công thức tính độ dài cung tròn.

Lời giải chi tiết:

a) Độ dài của cung tròn có số đo bằng 1 rad là bằng bán kính R.

b) Độ dài l của cung tròn có số đo $\alpha$ rad: $l = R\alpha$.

VD 1

Trạm vũ trụ Quốc tế ISS (tên Tiếng Anh: International Space Station) nằm trong quỹ đạo tròn cách bề mặt Trái Đất khoảng 400 km (H.1.1). Nếu trạm mặt đất theo dõi được trạm vũ trụ ISS khi nó nằm trong góc 45° ở tâm của quỹ đạo tròn này phía trên ăng-ten theo dõi, thì trạm vũ trụ ISS đã di chuyển được bao nhiêu kilômét trong khi nó đang được trạm mặt đất theo dõi? Giả sử rằng bán kính của Trái Đất là 6 400 km. Làm tròn kết quả đến hàng đơn vị.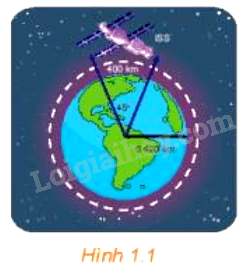

Phương pháp giải:

Một cung của đường tròn bán kính R và số đo $\alpha$ rad thì có độ dài $l = R\alpha$.

Lời giải chi tiết:

Bán kính quỹ đạo của trạm vũ trụ quốc tế là R = 6 400 + 400 = 6 800 (km).

Đổi $45{}^\circ =45\cdot \frac{\pi }{180}=\frac{\pi }{4}$.

Vậy trong khi được trạm mặt đất theo dõi, trạm ISS đã di chuyển một quãng đường có độ dài là $l = R\alpha \text{ = }6\,800\cdot \frac{\pi }{4}\approx 5\,340,708\approx 5\,341\,(km)$.