Giải mục 2 trang 50, 51, 52 SGK Toán 8 - Cùng khám phá

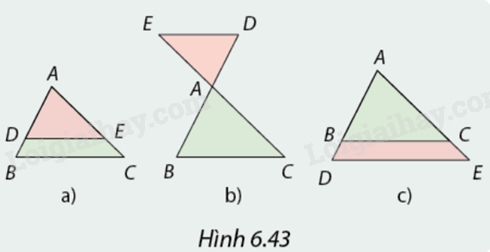
Hoạt động 2

Vẽ tam giác \(ABC\) bất kì. Vẽ đường thẳng song song với \(BC,\) cắt \(AB\) tại \(D,AC\) tại \(E\) (Hình 6.43). Theo em, tam giác \(ADE\) có đồng dạng với tam giác \(ABC\) không?

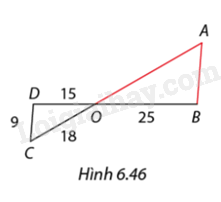
Phương pháp giải:

Dựa vào định nghĩa về tam giác đồng dạng để đưa ra dự đoán.

Lời giải chi tiết:

Theo em, tam giác \(ADE\) có đồng dạng với tam giác \(ABC\) .

Luyện tập 3

Trong Hình 6.46, \(AB\) và \(CD\) song song với nhau. Tìm độ dài \(AO\) và \(AB.\) 

Phương pháp giải:

Dựa vào định lí: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.

Lời giải chi tiết:

Xét hai tam giác \(ABO\) và \(CDO\) , ta có:

 \(CD\) cắt \(OB\) tại D

 \(CD\) cắt \(OA\) tại C

 \(CD//AB\)

Áp dụng định lí hai tam giác đồng dạng suy ra \(\Delta ABO\) ∽ \(\Delta CDO\)

 \(\begin{array}{l} \Rightarrow \frac{{DO}}{{BO}} = \frac{{CO}}{{AO}} = \frac{{CD}}{{AB}}\\ \Leftrightarrow \frac{{15}}{{25}} = \frac{{18}}{{AO}} = \frac{9}{{AB}}\\ \Rightarrow AO = 30;AB = 15\end{array}\) 

Vận dụng

Cánh buồm trên thực tế và ảnh chụp của nó \(\left( {\Delta ABC} \right)\) trong hình 6.47 có thể xem là hai tam giác vuông đồng dạng. Độ dài ba cạnh của cánh buồm trên ảnh chụp là \(3,3cm;3,5cm\) và \(1,6cm.\) Trên thực tế, cạnh ngắn nhất của cánh buồm là \(4m.\) Tính độ dài hai cạnh còn lại của cánh buồm theo đơn vị mét (làm tròn kết quả đến hàng phần mười).

Phương pháp giải:

Tam giác \(A'B'C'\) được gọi là đồng dạng với tam giác \(ABC\) , kí hiệu \(\Delta A'B'C'\) ∽ \(\Delta ABC\)

 \(\widehat {A'} = \widehat A;\widehat {B'} = \widehat B;\widehat {C'} = \widehat C\) và \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) .

Lời giải chi tiết:

Gọi cánh buồm trên thực tế là \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\) , ta có:

 \(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\\\frac{{A'B'}}{{3,3}} = \frac{{A'C'}}{{3,5}} = \frac{4}{{1,6}}\\ \Rightarrow A'B' = 8,25\left( m \right)\\ \Rightarrow A'C' = 8,75\left( m \right)\end{array}\)